Fixat figurer för alla pulser i scilab. Redigerat in designators och pilar etc. Lagt till ett clean script. Lagt till en refererad artikel.

rapport/clean.sh

@@ -0,0 +1 @@
+rm *.aux *.bbl *.bcf *.lof *.lot *.out *.blg *.log *.toc *.run.xml

rapport/discussion.tex

@@ -40,7 +40,7 @@ As can be seen in \autoref{tab:initial-measurements} and \autoref{tab:initial-me
 
 \section{Method}
 
-It was suprisingly difficult to find and choose apropriate components for the dummy load. The resistors had to tolerate extreme surges and the relays had to have high insulation voltages between the contacts.
+It was suprisingly difficult to find and choose apropriate components for the dummy load. The resistors had to tolerate extreme surges and the relays had to have high insulation voltages between the contacts. Even finding the encapsulation for the relay box proved to be a challenge, since the filtering options available at the retailers web stores were not always consistent.
 
 
 \subsection{Dummy Loads}
@@ -48,9 +48,9 @@ The results are well within the \SI{1}{\percent} specified by the standard \cite
 
 \subsection{Attenuators}
 \label{discussion_attenuators}
-During the project, the attenuation was considered as the voltage attenuation $att = 20 log_{10}\left( \frac{V_{in}}{V_{out}} \right)  \si{\deci\bel}$. However, lots of information and many tools for RF applications, including the calculator used for the attenuators in this project, assume power attenuation $att = 10 log_{10}\left( \frac{P_{in}}{P_{out}} \right)  \si{\deci\bel}$. The result of these two properties coincides when the input and output impedance, as well as the driving and loading impedance, are all the same.
+During the project, the attenuation was considered as the voltage attenuation \mbox{$att = 20 log_{10}\left( \frac{V_{in}}{V_{out}} \right)  \si{\deci\bel}$}. However, lots of information and many tools for RF applications, including the calculator used for the attenuators in this project, assume power attenuation \mbox{$att = 10 log_{10}\left( \frac{P_{in}}{P_{out}} \right)  \si{\deci\bel}$}. The result of these two properties coincides when the input and output impedance, as well as the driving and loading impedance, are all the same.
 
-The fact that these two ways of expressing attenuation could be mixed up was not noticed until very late in the project. Thus the values provided by the online attenuator tool did not give the desired results in the simulator, for the \SI{1000}{\ohm} attenuator. This was at the time manually tweaked until the desired attenuation was acquired, but the out impedance was not considered during the tweaking and ended thereby up being a bit mismatched for the next $\Pi$ link.
+The fact that these two ways of expressing attenuation could be mixed up was not noticed until very late in the project. Thus the values provided by the online attenuator tool did not give the desired results in the simulator, for the \SI{1000}{\ohm} attenuator. This was at the time manually tweaked until the desired attenuation was acquired, but the out impedance was not considered during the tweaking and thereby ended up being a bit mismatched for the next $\Pi$ link.
 
 There are infinitely many constellations to approximate the nominal value, in this project it was tried to use as few resistors as possible. This process was performed manually, since no suitable software for solving the problem was found. Thus the chosen constellations might not be optimal.
 

rapport/intro.tex

@@ -67,6 +67,7 @@ This paper only considers Pulse 1, Pulse 2a, Pulse 3a, Pulse 3b and Load dump A.
 This paper only considers the test equipment for ISO~7637-2 that was available at the company, presented in \autoref{tab:used_equipment}, for the pratical tests.
 \begin{table}[H]
     \centering
+    \caption{The test equipment available for the project}
     \begin{tabularx}{0.7\textwidth}{|l|l|X|}
         \hline
         \textbf{Brand} &\textbf{Model} &\textbf{Description}\\
@@ -80,7 +81,6 @@ This paper only considers the test equipment for ISO~7637-2 that was available a
         EMTEST		&CNA 200B    &Coupling network\\
         \hline
     \end{tabularx}    
-    \caption{The test equipment available for the project}
     \label{tab:used_equipment}
 \end{table}
 

rapport/main.tex

@@ -56,14 +56,19 @@
 %%% Put text inside a square %%%
 \newcommand{\squareit}[1]{\fbox{\parbox{\textwidth}{#1}}}
 
+% For the use of \nobreakdash-
+\usepackage{amsmath}
+
+%%% Non breaking prints of the ISO standards
+\newcommand{\nd}{\nobreakdash-}
+
+
 % Tables something?
 \usepackage{tabularx}
 
-
 % For H placement in figures
 \usepackage{float}
 
-
 % To be able to adjust caption with using \captionsetup{width=.8\linewidth}, also subfigures
 \usepackage{graphicx,caption}
 
@@ -73,6 +78,9 @@
 % Makes DOI numbers to links
 \usepackage{doi}
 
+% For the use of \nobreakdash-
+\usepackage{amsmath}
+
 % The footnotes are renumbered for each page
 \usepackage[perpage]{footmisc}
 
@@ -85,7 +93,6 @@
 %% For highlighting using \hl
 \usepackage{color,soul}
 
-
 % Use SI units
 \usepackage{siunitx}
 

rapport/method.tex

@@ -37,7 +37,7 @@ This chapter covers the methodologies used during the project.
 \section{Prestudy}
 During the project efforts were made to find relevant research using Linköping University Library's\footnote{\url{https://liu.se/en/library}} and Google Scholar's\footnote{\url{https://scholar.google.se/}} search engines. Among the keywords used in searching were;
 
-\squareit{ \emph{verification equipment}, \emph{test equipment}, \emph{automatic test}, \emph{automatic verification}, \emph{iso equipment}, \emph{electrical verification}, \emph{curve fitting}, \emph{double exponential function}, \emph{}, \emph{}}
+\squareit{ \emph{verification equipment}, \emph{test equipment}, \emph{automatic test}, \emph{automatic verification}, \emph{iso equipment}, \emph{electrical verification}, \emph{curve fitting}, \emph{double exponential function}, \emph{ISO 7637}, \emph{ISO 16750}}
 
 \todo[Skriv färdigt nyckelordsdelen och presera dem på ett snyggt men platseffektivt sätt]
 
@@ -67,9 +67,11 @@ In either case, the following tasks should be considered if there is time:
 \end{enumerate}
 
 \section{Examination and initial measurement of the old equipment}
+\hl{Peta in här någonstans att det var lite krångel att få fart på utrustningen och att det behövdes en del felsökning?}
+
 To decide the forthcoming of the project, the equipment first had to be checked to see if its performance were within the limits for use with the newer standard. Because there is no dummy loads available at this point of the project, only open load measurements could be done.
 
-With exception for Pulse 3a and Pulse 3b, all of these pulses were measured with the use of the high voltage differential probe described in \autoref{sec:hv-diff-probe}. The pulses are measured both directly on each generator connected according to \autoref{fig:manual-measurement-hv-diff} and also through the coupling network CNA~200, as depicted in \autoref{fig:manual-measurement-hv-diff-cna}. 
+With exception for Pulse 3a and Pulse 3b, all of the pulses were measured with the use of the high voltage differential probe described in \autoref{sec:hv-diff-probe}. The pulses are measured both directly on each generator connected according to \autoref{fig:manual-measurement-hv-diff} and also through the coupling network CNA~200, as depicted in \autoref{fig:manual-measurement-hv-diff-cna}. 
 \todo[figure of connection]
 Pulse 3a and Pulse 3b was measured using the attenuators described in \autoref{sec:hv-attenuators} connected according to \autoref{fig:manual-measurement-hv-att}. Thanks to the 50-ohm attenuator this pulse could be measured in its matched state. The measurement in open state is a compromise, since there was no such attenuator available, and was made into a 1000-ohm attenuator instead.
 
@@ -131,6 +133,7 @@ One manufacturer of thick film resistors, namely Vishay, specifies its overload
 The voltages used in the calculations are specified in \autoref{tab:dummy_load_worst_case}, they are slightly higher than the specified voltages on the equipment to allow for some margins. The worst case voltage must always be tolerated to prevent arching or serious degrading of the components.
 
 \begin{table}[h]
+    \caption{Calculated momentary worst cases for each dummy load.}
 \begin{adjustbox}{width=\columnwidth,center}
     \centering
     \begin{tabular}{|l|r|r|r|r|r|r|} 
@@ -144,7 +147,6 @@ The voltages used in the calculations are specified in \autoref{tab:dummy_load_w
         \hline
     \end{tabular}
 \end{adjustbox}
-    \caption{Calculated momentary worst cases for each dummy load.}
     \label{tab:dummy_load_worst_case}
 \end{table}
 \todo[Rätta till värdena i tabellen!]
@@ -194,7 +196,7 @@ With the minimum number of discrete resistors needed for each ideal resistor kno
 When the number of resistors and its constellations was decided, all of the discrete ideal resistors were replaced with non-ideal models in the simulation software. Then the attenuators were checked in frequency domain, as well as how the pulses were affected in time domain.
 
 \subsection{PCB for the relay box}
-\todo[Fin bild på designprocess av PVB, säkerhetsavstånd etc]
+\todo[Fin bild på designprocess av PCB, säkerhetsavstånd etc]
 
 Since the attenuators consits of SMD, surface-mount device, resistors, it was decided to design a PCB for this purpose. This also gives good control of the lengths of the conductors, which is of importance when designing for higher frequencies.
 

rapport/results.tex

@@ -42,6 +42,7 @@ Since not much was known about the project at this time, it was difficult to fin
 The result from the initial measurements are presented, along with the limits, in \autoref{tab:initial_measurements} without the CNA~200 connected and in \autoref{tab:initial_measurements_cna} with the CNA~200 connected.
 
 \begin{table}[h]
+    \caption{The initial manual measurements, measured directly at each generator's output.}
 \begin{adjustbox}{width=\columnwidth,center}
     %\centering
     \begin{tabular}{|l|r|r|r|r|r|r|} 
@@ -61,11 +62,11 @@ The result from the initial measurements are presented, along with the limits, i
         \hline
     \end{tabular}
 \end{adjustbox}
-    \caption{The initial manual measurements, measured directly at each generator's output.}
     \label{tab:initial_measurements}
 \end{table}
 
 \begin{table}[h]
+    \caption{The initial manual measurements on the equipment, including the CNA~200.}
 \begin{adjustbox}{width=\columnwidth,center}
     %\centering
     \begin{tabular}{|l|r|r|r|r|r|r|} 
@@ -85,7 +86,6 @@ The result from the initial measurements are presented, along with the limits, i
         \hline
     \end{tabular}
 \end{adjustbox}
-    \caption{The initial manual measurements on the equipment, including the CNA~200.}
     \label{tab:initial_measurements_cna}
 \end{table}
 
@@ -104,7 +104,9 @@ The 3rd alternative was chosen because of the convenience of a fully automatic s
 The resistance at the dummy loads are presented in \autoref{tab:four-wire-result}.
 
 \begin{table}[h]
-%\begin{adjustbox}{width=\columnwidth,center}
+    \captionsetup{width=.6\linewidth}
+    \caption{The measured resistance of the dummy loads, and the tolerance compared to the nominal values.}
+%\begin{adjustbox}{width=0.6\columnwidth,center}
     \centering
     \begin{tabular}{|l|r|r|} 
         \hline
@@ -116,7 +118,6 @@ The resistance at the dummy loads are presented in \autoref{tab:four-wire-result
         \hline
     \end{tabular}
 %\end{adjustbox}
-    \caption{The measured resistance of the dummy loads, and the tolerance compared to the nominal values.}
     \label{tab:four-wire-result}
 \end{table}
 
@@ -174,8 +175,8 @@ The \SI{60.1}{\deci\bel} attenuator was divided into one \SI{27.35}{\deci\bel} $
 		\includegraphics[width=\textwidth]{1k_gooc}
 		\caption{Ground terminal open, all other closed}
 	\end{subfigure}
+	\caption{The S21 measurements for the attenuators}
 	
-	\caption{The measurements made for the attenuators}
 \end{figure}
 
 \section{Analysis}

rapport/theory.tex

@@ -74,7 +74,7 @@ The test pulses of interest defined in ISO~7637 are denoted \emph{Test pulse 1},
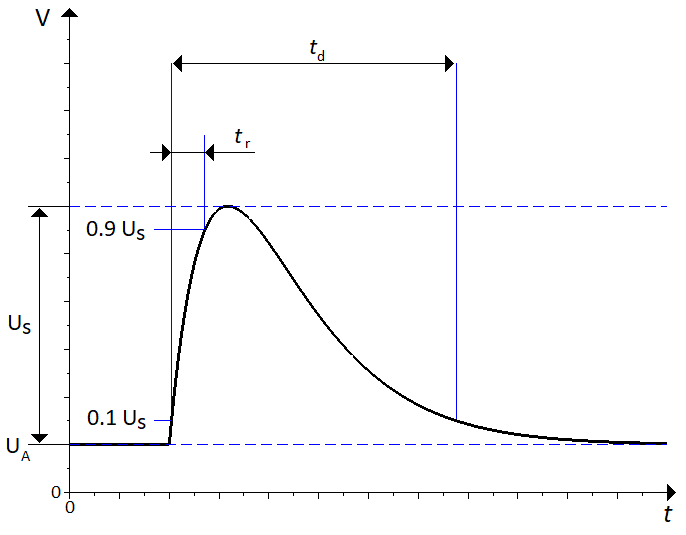
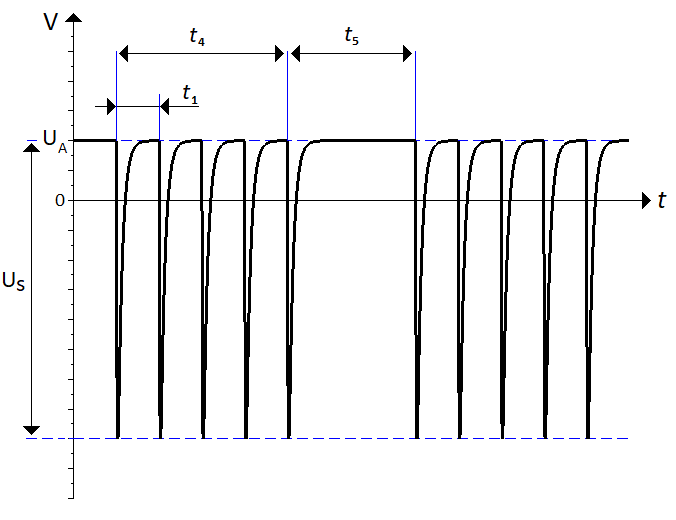
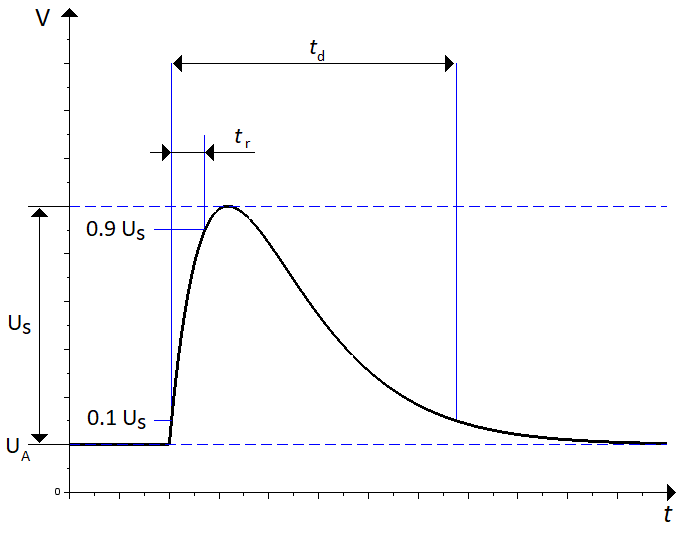
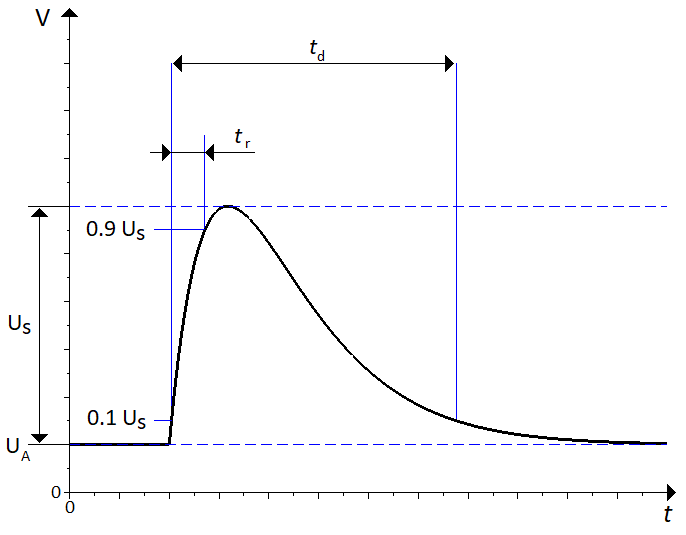
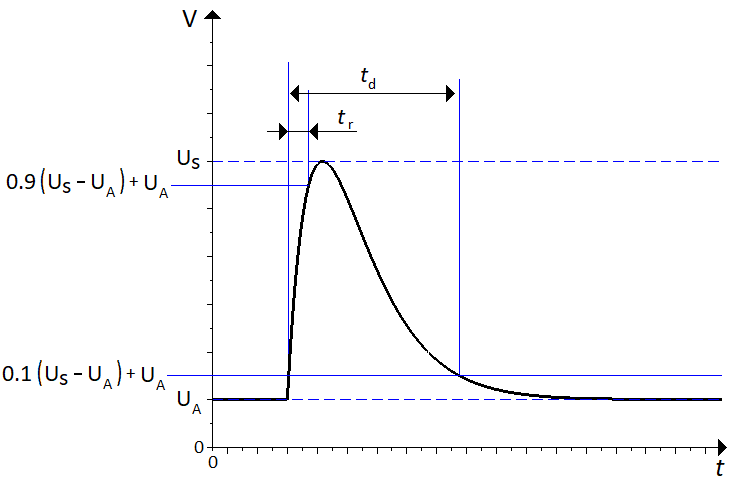
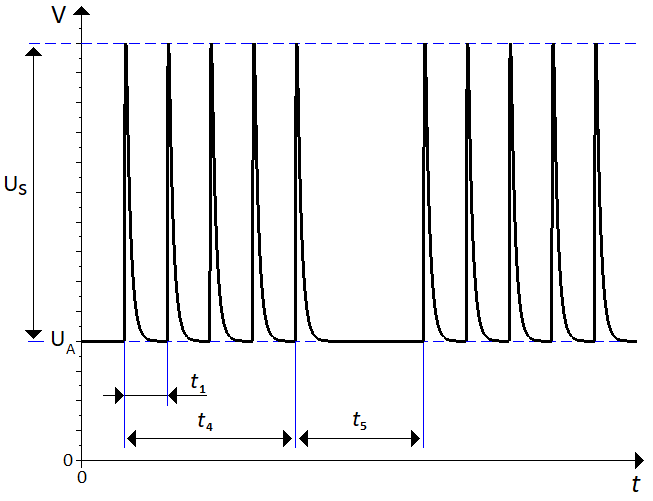
 The general characteristics in common for all pulses are the DC voltage $U_A$, the surge voltage $U_s$, the rise time $t_r$, the pulse duration $t_d$ and the internal resistance $R_i$. The internal resistance is only in series with the pulse generator, not the DC power source. For pulses that are supposed to be applied several times, $t_1$ usually denotes the time between the start of two consecutive pulses. The timings are illustrated in  \autoref{doubleexpfunc}.
 
 
-\begin{figure}
+\begin{figure}[h]
 	\centering
 	\begin{subfigure}[t]{0.45\textwidth}
 	    \includegraphics[width=\textwidth]{doubleexpfunc}
@@ -83,33 +83,147 @@ The general characteristics in common for all pulses are the DC voltage $U_A$, t
 	\end{subfigure}\hfill
 	\begin{subfigure}[t]{0.45\textwidth}
 	    \includegraphics[width=\textwidth]{doubleexpfuncrep}    
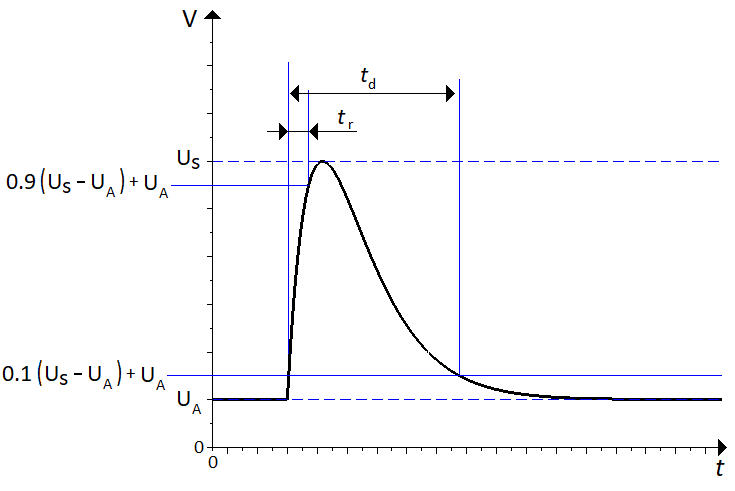
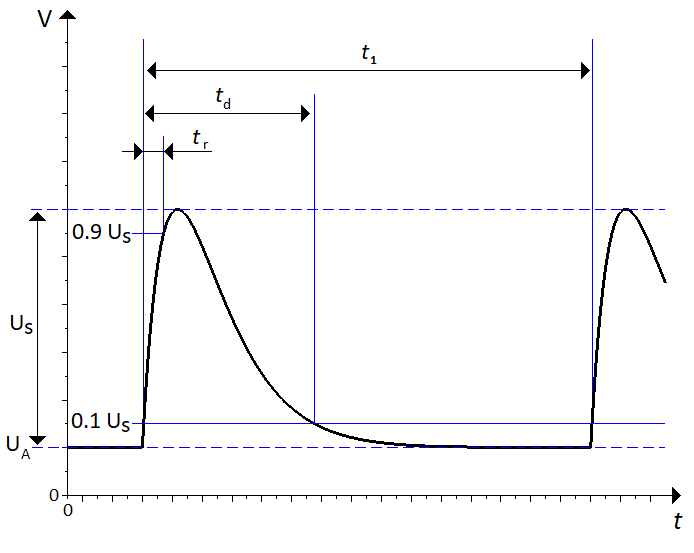
-	    \caption{The repetition time is defined as the time between two adjacent rising edges, measured at 0.1 times the maximum pulse voltage.}
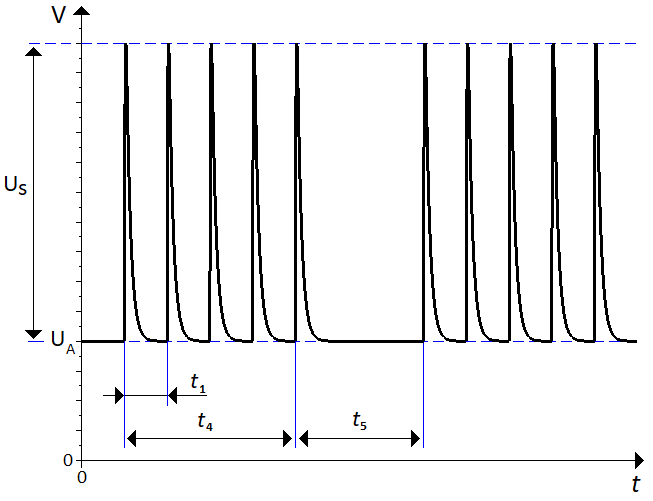
+	    \caption{The repetition time is defined as the time between two adjacent rising edges.}
    	    \label{fig:doubleexprep}
 	\end{subfigure}
 	\caption{The common properties of the pulses.}
 \end{figure}
 
-\todo[fixa referens till rätt kapitel]
 An important observation is that the definition of the surge voltage, $U_s$, differs in ISO~7637 and ISO~16750 as seen in \autoref{sec:us_difference}. \hl{In this report, only the definition from ISO~7637 is used.}
 
+\todo[Se till att fixa till referenserna här]
+\todo[Bestäm mig ifall jag ska använda båda definitionerna av $U_S$ eller bara ena]
+
 \subsection{Test pulse 1}
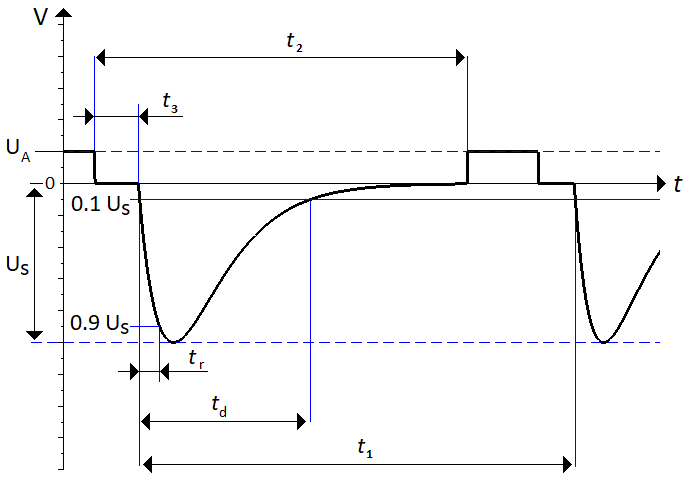
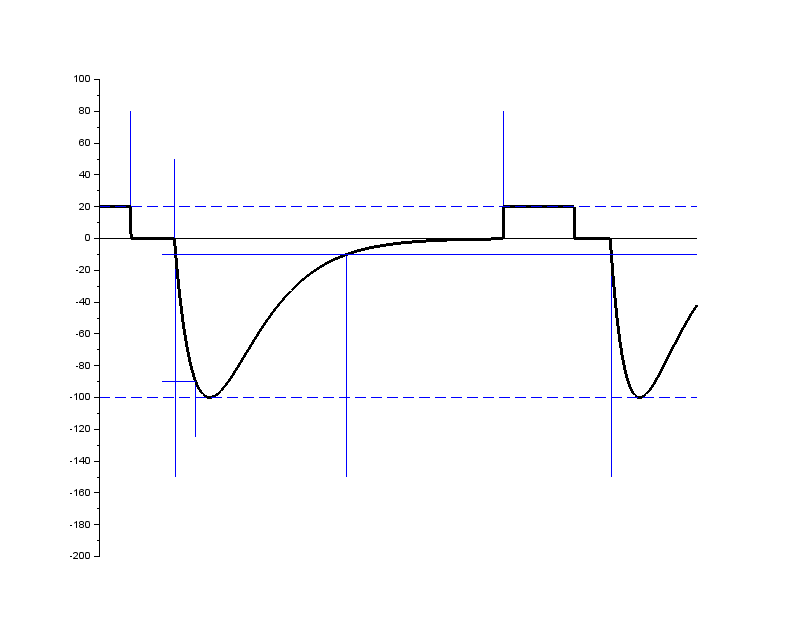
 This pulse simulates the event of the power supply being disconnected while the DUT is connected to other inductive loads. This leads to the other inductive loads generating a voltage transient of reversed polarity to the DUT's supply lines.
 
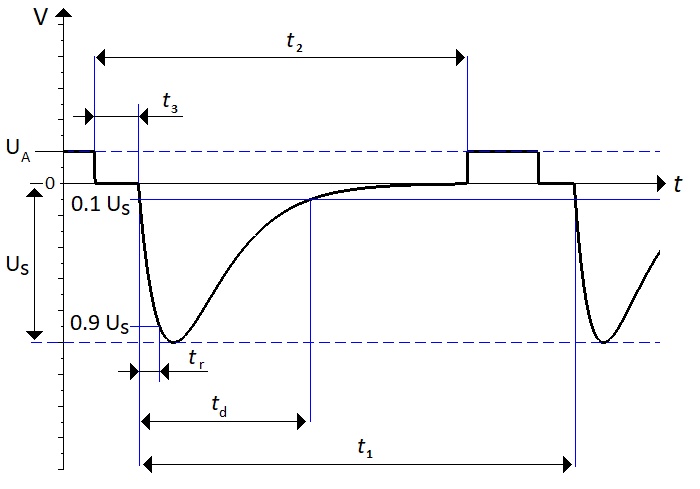
 In the standard there are two additional timings associated to this pulse, $t_2$ and $t_3$, which are defining the disconnection time for the power supply during the voltage transient. In practice $t_3$ can be very short, specified to less than 100 µs, and the step seen in \autoref{fig:pulse1} might be too short to be clearly distinguishable when seen on a oscilloscope.
 
-\todo[Två bilder, en på kurvan och en på kretsen som orsakar den. En tabell med parametervärden.]
+\begin{figure}[h]
+    %\captionsetup{width=.5\linewidth}
+    \centering
+    \includegraphics[width=\textwidth]{pulse1}    
+    \caption{Illustration of test pulse 1.}
+    \label{fig:pulse1}
+\end{figure}
+
+\begin{table}[h]
+    \centering
+    \caption{Parameter values for pulse 1}
+    \begin{tabularx}{0.7\textwidth}{|X|c|c|}
+        \hline
+        \textbf{Parameter}	&\textbf{\SI{12}{\volt} system}	&\textbf{\SI{24}{\volt} system}	\\
+        \hline
+        $U_A$			& \SIrange{13.8}{14.2}{\volt}	& \SIrange{27.8}{28.2}{\volt}	\\
+        \hline
+        $U_S$			& \SIrange{-75}{-150}{\volt}	& \SIrange{-300}{-600}{\volt}	\\
+        \hline
+        $R_i$				& \SI{10}{\ohm}				& \SI{50}{\ohm}				\\
+        \hline
+        $t_d$			& \SI{2}{\milli\second}			& \SI{1}{\milli\second}			\\
+        \hline
+        $t_r$				& \SIrange{0.5}{1}{\micro\second}	& \SIrange{1.5}{3}{\micro\second} \\
+        \hline
+        $t_1$ 			& \multicolumn{2}{c|}{$\geq$\SI{0.5}{\second}}				\\
+        \hline
+        $t_2$ 			& \multicolumn{2}{c|}{\SI{200}{\milli\second}} 				\\
+        \hline
+        $t_3$ 			& \multicolumn{2}{c|}{$<$\SI{100}{\micro\second}} 			\\
+        \hline
+    \end{tabularx}    
+    \label{tab:pulse1}
+\end{table}
+
+\todo[En bild på kretsen som orsakar pulsen.]
 
 \subsection{Test pulse 2a}
-This pulse simulates the event of a load, parallel to the DUT, being disconnected. The inductance in the wiring harness will then generate a positive voltage transient on the DUT's supply lines.
+This pulse simulates the event of a load, parallel to the DUT, being disconnected. The inductance in the wiring harness will then generate a positive voltage transient on the DUT's supply lines. distinguishable when seen on a oscilloscope.
+
+\begin{figure}[h]
+    %\captionsetup{width=.5\linewidth}
+    \centering
+    \includegraphics[width=\textwidth]{pulse2a}    
+    \caption{Illustration of test pulse 2a.}
+    \label{fig:pulse2a}
+\end{figure}
 
-\todo[Två bilder, en på kurvan och en på kretsen som orsakar den. En tabell med parametervärden.]
+\begin{table}[h]
+    \centering
+    \caption{Parameter values for pulse 2a}
+    \begin{tabularx}{0.7\textwidth}{|X|c|c|}
+        \hline
+        \textbf{Parameter}	&\textbf{\SI{12}{\volt} system}	&\textbf{\SI{24}{\volt} system}	\\
+        \hline
+        $U_A$			& \SIrange{13.8}{14.2}{\volt}	& \SIrange{27.8}{28.2}{\volt}	\\
+        \hline
+        $U_S$			&  \multicolumn{2}{c|}{\SIrange{37}{112}{\volt}}				\\
+        \hline
+        $R_i$				&  \multicolumn{2}{c|}{\SI{2}{\ohm}}						\\
+        \hline
+        $t_d$			&  \multicolumn{2}{c|}{\SI{0.05}{\milli\second}}				\\
+        \hline
+        $t_r$				&  \multicolumn{2}{c|}{\SIrange{0.5}{1}{\micro\second}}		\\
+        \hline
+        $t_1$ 			&  \multicolumn{2}{c|}{\SIrange{0.2}{5}{\second}}			\\
+        \hline
+    \end{tabularx}    
+    \label{tab:pulse2a}
+\end{table}
+
+\todo[En bild på kretsen som orsakar pulsen.]
 
 \subsection{Test pulse 3a and 3b}
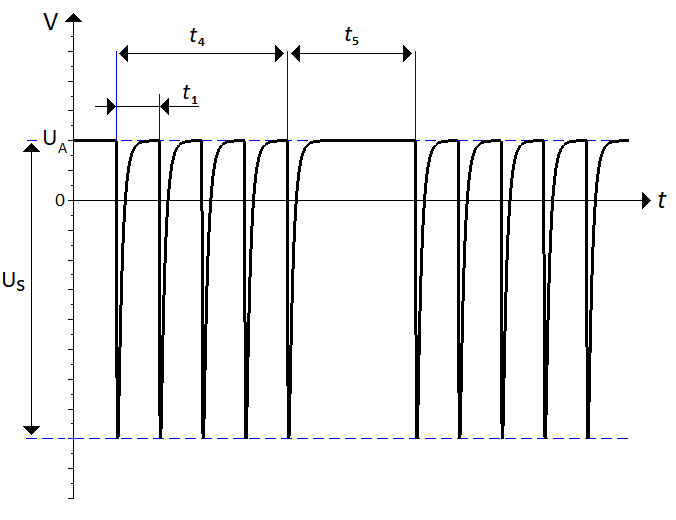
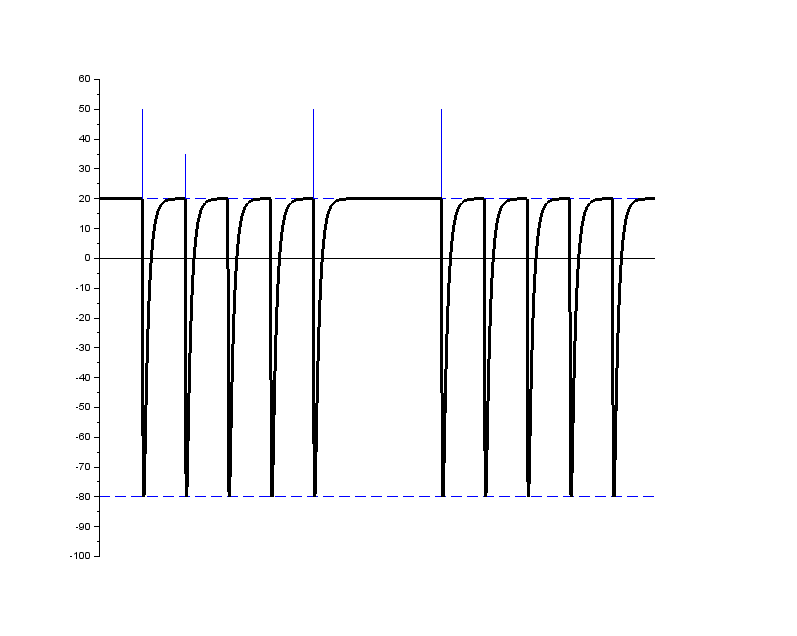
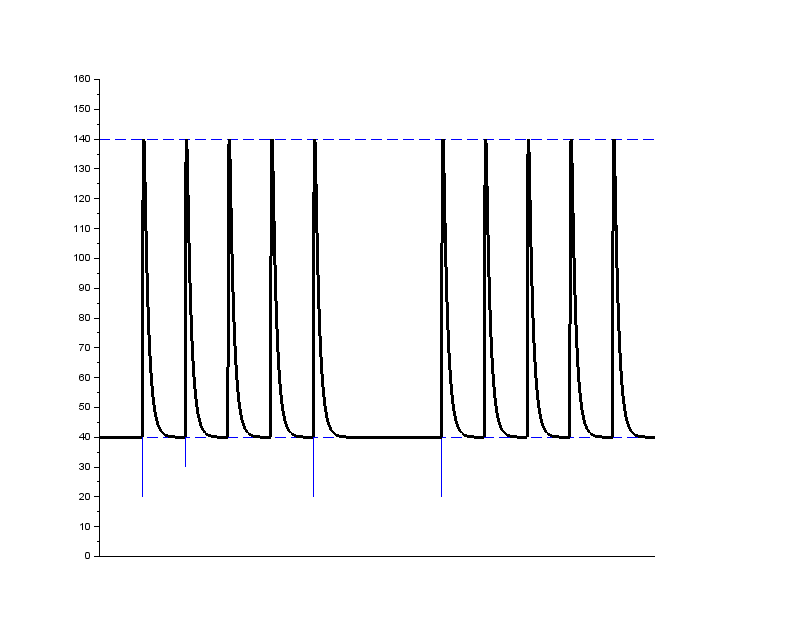
 Test pulse 3a and 3b simulates transients ``which occur as a result of the switching process'' as stated in the standard \cite{iso_7637_2}. The formulation is not very clear, but is interperted and explained by Frazier and Alles \cite{comparison_iso_7637_real_world} to be the result of a mechanical switch breaking an inductive load. These transients are very short, compared to the other pulses, and the repetition time is very short. The pulses are sent in bursts, grouping a number of pulses together and separating groups by a fixed time.
 
 These pulses contain high frequency components, up to 100~MHz, and special care must be taken when running tests with them as well as when verifying them.
 
-\todo[Fyra bilder, två på kurvorna, en på burst och en på kretsen som orsakar den? En tabell med parametervärden.]
+
+\begin{figure}[h]
+	\centering
+	\begin{subfigure}[t]{0.45\textwidth}
+	    \includegraphics[width=\textwidth]{pulse3a}
+	    \caption{Pulse 3a}
+   	    \label{fig:pulse3a}
+	\end{subfigure}\hfill
+	\begin{subfigure}[t]{0.45\textwidth}
+	    \includegraphics[width=\textwidth]{pulse3b}    
+	    \caption{Pulse 3b}
+   	    \label{fig:pulse3b}
+	\end{subfigure}
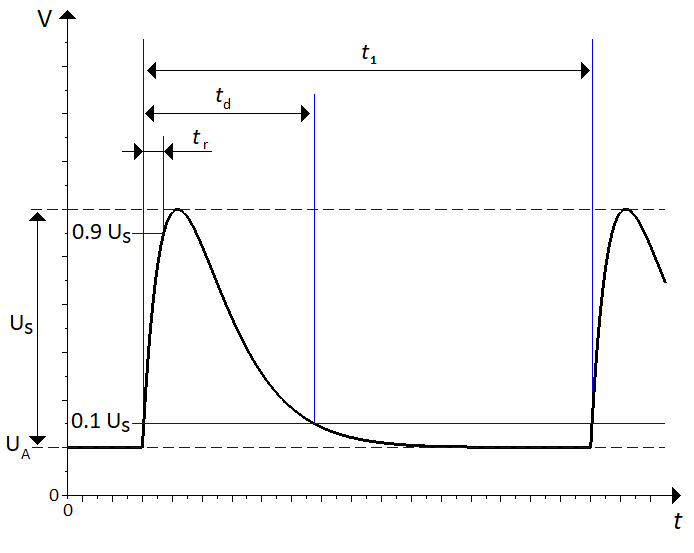
+	\caption{Pulse 3a and 3b are applied in bursts. Each individual pulse is a double exponential curve with the same properties, $t_r$ and $t_d$, as e.g. pulse 2a}
+	\label{fig:pulse3}
+\end{figure}
+
+\begin{table}[h]
+    \centering
+    \caption{Parameter values for pulse 3a and 3b}
+    \begin{tabularx}{0.7\textwidth}{|X|c|c|}
+        \hline
+        \textbf{Parameter}	&\textbf{\SI{12}{\volt} system}	&\textbf{\SI{24}{\volt} system}	\\
+        \hline
+        $U_A$			& \SIrange{13.8}{14.2}{\volt}	& \SIrange{27.8}{28.2}{\volt}	\\
+        \hline
+        Pulse 3a $U_S$		& \SIrange{-112}{-220}{\volt}	& \SIrange{-150}{-300}{\volt}	\\
+        \hline
+        Pulse 3b $U_S$		& \SIrange{75}{150}{\volt}		& \SIrange{150}{300}{\volt}	\\
+        \hline
+        $R_i$				&  \multicolumn{2}{c|}{\SI{50}{\ohm}}						\\
+        \hline
+        $t_d$			&  \multicolumn{2}{c|}{\SIrange{105}{195}{\nano\second}}		\\
+        \hline
+        $t_r$				&  \multicolumn{2}{c|}{\SIrange{3.5}{6.5}{\nano\second}}		\\
+        \hline
+        $t_1$			&  \multicolumn{2}{c|}{\SI{100}{\micro\second}}				\\
+        \hline
+        $t_4$			&  \multicolumn{2}{c|}{\SI{10}{\milli\second}}				\\
+        \hline
+        $t_5$			&  \multicolumn{2}{c|}{\SI{90}{\milli\second}}				\\
+        \hline
+    \end{tabularx}    
+    \label{tab:pulse3}
+\end{table}
+
+\todo[En bild på kretsen som orsakar pulsen.]
 
 \subsection{Load dump Test A}
 The Load dump Test A simulates the event of disconnecting a battery that is charged by the vehicles alternator, the current that the alternator is driving will give rise to a long voltage transient.
@@ -118,7 +232,38 @@ This pulse has the longest duration, $t_d$, of all the test pulses. It also has
 
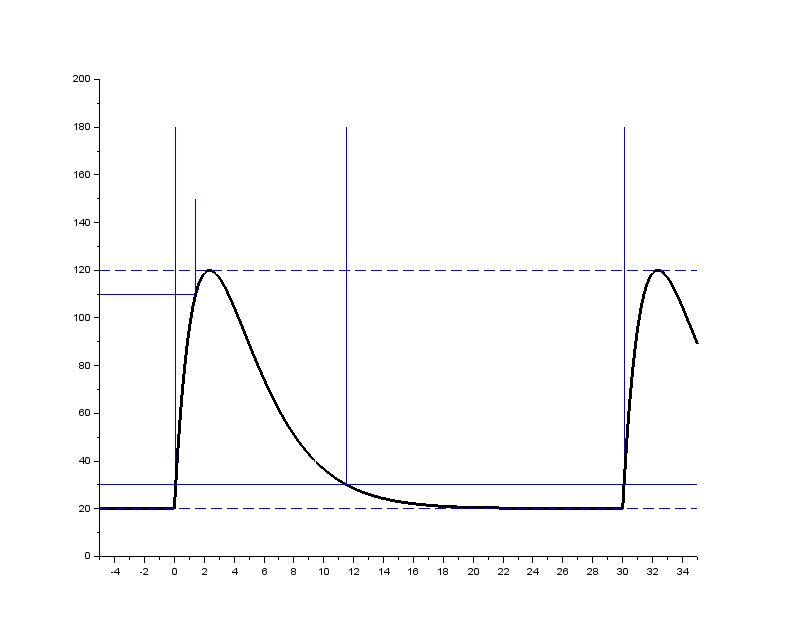
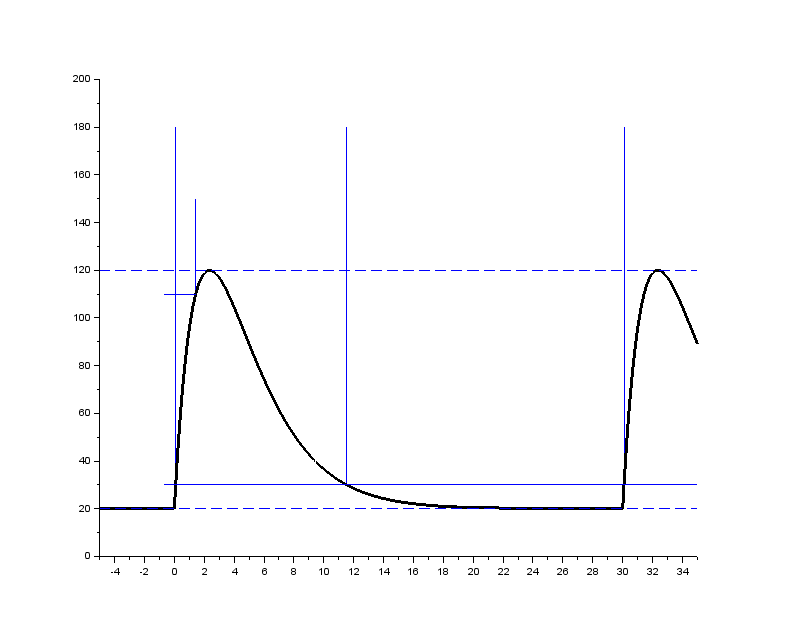
 Prior to 2011, the Load dump Test A was part of the ISO~7637-2 standard under the name \emph{Test pulse 5a}. The surge voltage $U_s$ was in the older standard, \mbox{ISO~7637-2:2004}, defined as the voltage between the DC offset voltage $U_A$ and the maximum voltage. In the newer standard, \mbox{ISO~16750-2:2012}, $U_s$ is defined as the absolute peak voltage. Only the former definition is used in this paper, $U_s = \hat{U} - U_A$.
 
-\todo[Två bilder, en på kurvan och en på kretsen som orsakar den. En tabell med parametervärden.]
+\begin{figure}[h]
+    %\captionsetup{width=.5\linewidth}
+    \centering
+    \includegraphics[width=\textwidth]{load dump a}
+    \caption{Illustration of load dump Test A. Note the difference of $U_S$ compared to all the other pulses. To minimize the risk of misunderstandings, only the way of specifying $U_S$ as the other pulses do will be used unless otherwise stated.}
+    \label{fig:loadDumpTestA}
+\end{figure}
+
+\begin{table}[h]
+    \centering
+    \caption{Parameter values for load dump Test A}
+    \begin{tabularx}{0.7\textwidth}{|X|c|c|}
+        \hline
+        \textbf{Parameter}	&\textbf{\SI{12}{\volt} system}		&\textbf{\SI{24}{\volt} system}		\\
+        \hline
+        $U_A$			& \SIrange{13.8}{14.2}{\volt}		& \SIrange{27.8}{28.2}{\volt}		\\
+        \hline
+        $U_S$ ISO~16750	& \SIrange{79}{101}{\volt}			& \SIrange{151}{202}{\volt}		\\	
+        \hline
+        $U_S$ ISO~7637	& \SIrange{64.8}{87.2}{\volt}		& \SIrange{122.8}{174.2}{\volt}		\\
+        \hline
+        $R_i$				& \SIrange{0.5}{4}{\ohm}			& \SIrange{1}{8}{\ohm}			\\
+        \hline
+        $t_d$			& \SIrange{40}{400}{\milli\second}	& \SIrange{100}{350}{\milli\second}	\\
+        \hline
+        $t_r$				& \multicolumn{2}{c|}{\SIrange{5}{10}{\milli\second}}					\\
+        \hline
+    \end{tabularx}    
+    \label{tab:loadDumpTestA}
+\end{table}
+
+\todo[En bild på kretsen som orsakar pulsen.]
 
 \subsection{Test setup}
 During a test, the nominal voltage is first applied between the plus and minus terminal of the DUT's power supply input. Then a series of test pulses are applied between the same terminals. The pulses are repeated at specified intervals, $t_1$, as depicted in \autoref{fig:doubleexprep}.
@@ -132,6 +277,7 @@ The verification is to be conducted with $U_A$ set to 0. There is, however, a pr
 The limits, and tolerances, for the pulses are summarised in \autoref{tab:verification-list}. The matched loads are to be within 1\% of the nominal value. \cite{iso_7637_2}
 
 \begin{table}[h]
+    \caption{These are all of the verifications that needs to be made before each use of the equipment, along with the limits for each case.}
 \begin{adjustbox}{width=\columnwidth,center}
     %\centering
     \begin{tabular}{|l|r|r|r|r|} 
@@ -139,7 +285,7 @@ The limits, and tolerances, for the pulses are summarised in \autoref{tab:verifi
          & & \multicolumn{3}{c|}{Limits}\\
         Pulse & Match resistor (\si{\ohm}) & $U_S$ (\si{\volt}) & $t_d$ (\si{\second}) & $t_r$ (\si{\second}) \\
         \hline
-        Pulse 1, 12 V, Open         &    & $[ -110, -90 ]$   & $[1.6,2.4]$ \si{\milli}   & $[0.5,1]$ \si{\micro}     \\
+        Pulse 1, 12 V, Open         &    & $[ -110, -90 ]$   & \SIrange{1.6}{2.4}{\milli\second} $[1.6,2.4]$ \si{\milli}   & $[0.5,1]$ \si{\micro}     \\
         Pulse 1, 12 V, Matched      & 10 & $[ -110, -90 ]$   & $[1.6,2.4]$ \si{\milli}   & $[0.5,1]$ \si{\micro}     \\
         Pulse 1, 24 V, Open         &    & $[ -660, -540 ]$  & $[0.8,1.2]$ \si{\milli}   & $[1.5,3]$ \si{\micro}     \\
         Pulse 1, 24 V, Matched      & 50 & $[ -660, -540 ]$  & $[0.8,1.2]$ \si{\milli}   & $[1.5,3]$ \si{\micro}     \\
@@ -156,42 +302,38 @@ The limits, and tolerances, for the pulses are summarised in \autoref{tab:verifi
         \hline
     \end{tabular}
 \end{adjustbox}
-    \caption{These are all of the verifications that needs to be made before each use of the equipment, along with the limits for each case.}
     \label{tab:verification-list}
 \end{table}
 
 \section{Differences between the new and the old standard}
-Since the equipment used the project is designed for the older version of the standard, ISO~7637-2:2004 and possibly even ISO~7637-1:1990 together with ISO~7637-2:1990, the differences of importance between these will be presented in this chapter to see what parameters might be a problem for the older equipment to fulfil.
+Since the equipment used the project is designed for the older version of the standard, ISO~7637\nd2:2004 and possibly even ISO~7637\nd1:1990 together with ISO~7637\nd2:1990, the differences of importance between these will be presented in this chapter to see what parameters might be a problem for the older equipment to fulfil.
 
-One of the most notable differences is the removal of a test pulse from ISO~7637-2 that was called \emph{Pulse 5a} and \emph{Pulse 5b}, this was instead introduced to the ISO~16750-2 under the name \emph{Load dump A} and \emph{Load dump B}.
+One of the most notable differences is the removal of a test pulse from ISO~7637\nd2 that was called \emph{Pulse 5a}, this was instead introduced to the ISO~16750\nd2 under the name \emph{Load dump A}.
 
 \subsection{Supply voltage}
+The definition of the DC supply voltage for the DUT differs in some case between the older and the newer versions of the standard. There are two different supply voltage definitions. $U_A$ represents a system where the generator is in operation and $U_B$ represents the system without the generator in operation. These have different values for \SI{12}{\volt} and \SI{24}{\volt} systems. $U_B$ is only relevant for Load dump Test A and is thus not defined in ISO~7637 anymore.
 
-\textbf{ISO 7637-2:2004}
-
-12V: $U_A = 13.5 \pm 0.5$
-
-12V: $U_B = 12.5 \pm 0.2$
-
-24V: $U_A = 27 \pm 1$
-
-24V: $U_B = 24 \pm 0.4$
-
-\textbf{ISO 7637-1:2015}
-
-12V: $U_A = 13 \pm 1$
-
-24V: $U_A = 26 \pm 2$
-
-\textbf{ISO 16750-1}
-
-12V: $U_A = 14 \pm 0.2$
+In the older ISO~7637 the definitions could be found in part 2 in clause 4.2. In the newer version these were moved to part 1, clause 5.3. The definition of $U_B$ was moved to ISO~16750\nd1: \hl{SE TILL ATT KOLLA I VILKA KAPITEL I VILKA STANDARDER SAKERNA STÅR NÅGONSTANS}
 
-12V: $U_B = 12.5 \pm 0.2$
-
-24V: $U_A = 28 \pm 0.2$
-
-24V: $U_B = 24 \pm 0.2$
+\begin{table}[h]
+    \caption{Comparison of the different supply voltage definitions.}
+\begin{adjustbox}{width=\columnwidth,center}
+    %\centering
+    \begin{tabular}{|l|l|r|r|r|} 
+        \hline
+         &    & \multicolumn{3}{c|}{Supply voltage range}    \\
+        Parameter & $U_N$    & ISO 7637-2:2004    & ISO 7637-1:2015 &    ISO 16750-1:2018    \\
+        \hline
+       $U_A$    & \SI{12}{\volt}    & \SIrange{13}{14}{\volt}    & \SIrange{12}{13}{\volt} &    \SIrange{13.8}{14.2}{\volt}    \\
+       $U_A$    & \SI{24}{\volt}    & \SIrange{26}{28}{\volt}    & \SIrange{24}{28}{\volt} &    \SIrange{27.8}{28.2}{\volt}    \\
+       \hline
+       $U_B$    & \SI{12}{\volt}    & \SIrange{12.3}{12.7}{\volt}    & -    &    \SIrange{12.3}{12.7}{\volt}    \\
+       $U_B$    & \SI{24}{\volt}    & \SIrange{23.6}{24.4}{\volt}    & -    &    \SIrange{23.8}{24.2}{\volt}    \\
+        \hline
+    \end{tabular}
+\end{adjustbox}
+    \label{tab:supplyVoltageDiff}
+\end{table}
 
 \subsection{Definitions}
 ISO~7637 and ISO~16750

scilab/pulses/load dump a.sce

@@ -0,0 +1,125 @@
+xdel(winsid())
+clear;
+
+t = linspace(-5,20,5000);
+a = 0.4;
+b = 0.45;
+k = 1;
+
+magnitude = 100;
+offset = 20
+
+// Generera självaste pulsformen
+y = k*(exp(-a*t) - exp(-b*t) );
+
+// Fyll på med lite platt mark före t=0
+y(y<0) = 0;
+
+// Normalisera till 1 och multiplicera med magnituden
+y = y/max(y)*magnitude;
+
+// Hitta index för första passagen av 10%
+x10r = 0;
+for i = [1:length(y)]
+    if(y(i) > 0.1*magnitude)
+        if((y(i)-0.1*magnitude) < (0.1*magnitude-y(x10r)))
+            x10r = i;
+        end;
+        break;
+    end;
+    x10r = i;
+end
+
+// Hitta index för första passagen av 90%
+x90r = 0;
+for i = [1:length(y)]
+    if(y(i) > 0.9*magnitude)
+        if((y(i)-0.9*magnitude) < (0.9*magnitude-y(x90r)))
+            x90r = i;
+        end;
+        break;
+    end;
+    x90r = i;
+end
+
+// Hitta index för första passagen av 10%
+x10f = 0;
+for i = [length(y):-1:1]
+    if(y(i) > 0.1*magnitude)
+        if((y(i)-0.1*magnitude) < (0.1*magnitude-y(x10f)))
+            x10f = i;
+        end;
+        break;
+    end;
+    x10f = i;
+end
+
+// Lägg på ett offset
+y = y+offset;
+
+// Lägg på lite av nästa kurva, en kopia av dena kurvan
+y = [y y(1:2000)];
+t = [t linspace(25,25*(1+2/5), 2000)];
+
+//Generera vertikala linjer
+xpts = [1 1];
+//plot(xpts*0, ypts, '-black'); // Vertikalt streck på x = 
+ypts = [(0.1*magnitude+offset) max(y)*1.5];
+plot(xpts*t(x10r), ypts, '-'); // 10% rise
+plot(xpts*t(x10f), ypts, '-'); // 10% fall
+plot(xpts*t(x10r+5000), ypts, '-'); // second 10% rise
+ypts = [(0.9*magnitude+offset) max(y)*1.25];
+plot(xpts*t(x90r), ypts, '-'); // 90% rise
+
+// Generera horisontella linjer
+
+// Pulsen
+plot(t, y, "black");
+p = get("hdl");
+p = p.children;
+p.thickness = 3;
+
+// max och min horisontella
+hline = ones(1,length(t));
+plot(t,hline.*max(y), '--');
+plot(t,hline.*min(y), '--');
+plot(t,hline.*0, '-black');
+
+// 10 och 90% horizontella
+tshort = t(1:length(t))
+hline = ones(1,length(tshort));
+plot(tshort,hline.*y(x10r), '-');
+tshort = t(1:x90r)
+hline = ones(1,length(tshort));
+plot(tshort,hline.*y(x90r), '-');
+
+// titletxt = ['$y = k(e^{-\alpha t} - e^{-\beta t})$' ; strcat(['$k=', string(k), ', \alpha=', string(a), ', \beta=', string(b), '$']) ];
+
+//titletxt = '$u(t) = k(e^{-\alpha t} - e^{-\beta t})$';
+//title(titletxt , 'fontsize', 8);
+//xlabel('t (s)', 'fontsize', 7);
+//ylabel('U (V)', 'fontsize', 7, 'rotation', 0);
+
+a = get("current_axes");
+//a.axes_visible = "off";
+// Rita axlarna i 0
+//a.x_location = "origin";
+//a.y_location = "origin";
+
+
+// Bestäm viewport och ta bort inramning
+a.data_bounds = [min(t),0;max(t),200];
+a.box = "off";
+
+
+// Fula pilar (nästan) på axlarna
+//b = a.data_bounds
+//xstring(b(1),b(4),"↑")
+//set(gce(), "clip_state","off", "text_box_mode","centered", "font_size",4)
+//
+//xstring(b(2),b(3),"→")
+//set(gce(), "clip_state","off", "text_box_mode","centered", "font_size",4)
+
+f=get("current_figure")
+f.figure_size=f.figure_size*1.3  // Råkade bli lagom storlek
+

scilab/pulses/pulse1.sce

@@ -0,0 +1,133 @@
+xdel(winsid())
+clear;
+
+t = linspace(-5,25,5000);
+a = 0.4;
+b = 0.45;
+k = 1;
+
+magnitude = 100;
+offset = 20
+
+// Generera självaste pulsformen
+y = k*(exp(-a*t) - exp(-b*t) );
+
+// Fyll på med lite platt mark före t=0
+y(y<0) = 0;
+
+// Normalisera till 1 och multiplicera med magnituden
+y = y/max(y)*magnitude;
+
+// Hitta index för första passagen av 10%
+x10r = 0;
+for i = [1:length(y)]
+    if(y(i) > 0.1*magnitude)
+        if((y(i)-0.1*magnitude) < (0.1*magnitude-y(x10r)))
+            x10r = i;
+        end;
+        break;
+    end;
+    x10r = i;
+end
+
+// Hitta index för första passagen av 90%
+x90r = 0;
+for i = [1:length(y)]
+    if(y(i) > 0.9*magnitude)
+        if((y(i)-0.9*magnitude) < (0.9*magnitude-y(x90r)))
+            x90r = i;
+        end;
+        break;
+    end;
+    x90r = i;
+end
+
+// Hitta index för första passagen av 10%
+x10f = 0;
+for i = [length(y):-1:1]
+    if(y(i) > 0.1*magnitude)
+        if((y(i)-0.1*magnitude) < (0.1*magnitude-y(x10f)))
+            x10f = i;
+        end;
+        break;
+    end;
+    x10f = i;
+end
+
+// Lägg på ett offset
+y = y.*-1;
+y(1:350) = offset;
+y(length(y)-500:length(y)) = offset;
+
+// Lägg på lite av nästa kurva, en kopia av dena kurvan
+y = [y y(1:2000)];
+t = [t linspace(25,25*(1+2/5), 2000)];
+
+
+//Generera vertikala linjer
+xpts = [1 1];
+//plot(xpts*0, ypts, '-black'); // Vertikalt streck på x = 
+ypts = [(-0.1*magnitude) min(y)*1.5];
+plot(xpts*t(x10r),ypts, '-'); // Rise 10%
+plot(xpts*t(x10r+5000),ypts, '-'); // Second rise 10%
+plot(xpts*t(x10f), ypts, '-'); // Fall 10%
+ypts = [(-0.9*magnitude) min(y)*1.25];
+plot(xpts*t(x90r), ypts, '-'); // Rise 90%
+ypts = [offset offset*4];
+plot(xpts*t(350), ypts, '-'); // Supply off
+plot(xpts*t(4500), ypts, '-'); // Supply on
+ypts = [0 offset*2.5];
+plot(xpts*0, ypts, '-'); // Pulse start (zero)
+
+// Generera horisontella linjer
+
+// Pulsen
+plot(t, y, "black");
+p = get("hdl");
+p = p.children;
+p.thickness = 3;
+
+// max och min horisontella
+hline = ones(1,length(t));
+plot(t,hline.*max(y), '--');
+plot(t,hline.*min(y), '--');
+plot(t,hline.*0, '-black');
+
+// 10 och 90% horizontella
+tshort = t(x10r-150:length(t))
+hline = ones(1,length(tshort));
+plot(tshort,hline.*y(x10r), '-');
+tshort = t(x10r-150:x90r)
+hline = ones(1,length(tshort));
+plot(tshort,hline.*y(x90r), '-');
+
+// titletxt = ['$y = k(e^{-\alpha t} - e^{-\beta t})$' ; strcat(['$k=', string(k), ', \alpha=', string(a), ', \beta=', string(b), '$']) ];
+
+//titletxt = '$u(t) = k(e^{-\alpha t} - e^{-\beta t})$';
+//title(titletxt , 'fontsize', 8);
+//xlabel('t (s)', 'fontsize', 7);
+//ylabel('U (V)', 'fontsize', 7, 'rotation', 0);
+
+a = get("current_axes");
+//a.axes_visible = "off";
+a.axes_visible(1) = "off"; // Turn off X-axxis
+// Rita axlarna i 0
+//a.x_location = "origin";
+//a.y_location = "origin";
+
+
+// Bestäm viewport och ta bort inramning
+a.data_bounds = [min(t),-magnitude*1.6;max(t),magnitude];
+a.box = "off";
+
+// Fula pilar (nästan) på axlarna
+//b = a.data_bounds
+//xstring(b(1),b(4),"↑")
+//set(gce(), "clip_state","off", "text_box_mode","centered", "font_size",4)
+//
+//xstring(b(2),b(3),"→")
+//set(gce(), "clip_state","off", "text_box_mode","centered", "font_size",4)
+
+f=get("current_figure")
+f.figure_size=f.figure_size*1.3  // Råkade bli lagom storlek
+

scilab/pulses/pulse2a.sce

@@ -0,0 +1,125 @@
+xdel(winsid())
+clear;
+
+t = linspace(-5,20,5000);
+a = 0.4;
+b = 0.45;
+k = 1;
+
+magnitude = 100;
+offset = 20
+
+// Generera självaste pulsformen
+y = k*(exp(-a*t) - exp(-b*t) );
+
+// Fyll på med lite platt mark före t=0
+y(y<0) = 0;
+
+// Normalisera till 1 och multiplicera med magnituden
+y = y/max(y)*magnitude;
+
+// Hitta index för första passagen av 10%
+x10r = 0;
+for i = [1:length(y)]
+    if(y(i) > 0.1*magnitude)
+        if((y(i)-0.1*magnitude) < (0.1*magnitude-y(x10r)))
+            x10r = i;
+        end;
+        break;
+    end;
+    x10r = i;
+end
+
+// Hitta index för första passagen av 90%
+x90r = 0;
+for i = [1:length(y)]
+    if(y(i) > 0.9*magnitude)
+        if((y(i)-0.9*magnitude) < (0.9*magnitude-y(x90r)))
+            x90r = i;
+        end;
+        break;
+    end;
+    x90r = i;
+end
+
+// Hitta index för första passagen av 10%
+x10f = 0;
+for i = [length(y):-1:1]
+    if(y(i) > 0.1*magnitude)
+        if((y(i)-0.1*magnitude) < (0.1*magnitude-y(x10f)))
+            x10f = i;
+        end;
+        break;
+    end;
+    x10f = i;
+end
+
+// Lägg på ett offset
+y = y+offset;
+
+// Lägg på lite av nästa kurva, en kopia av dena kurvan
+y = [y y(1:2000)];
+t = [t linspace(25,25*(1+2/5), 2000)];
+
+//Generera vertikala linjer
+xpts = [1 1];
+//plot(xpts*0, ypts, '-black'); // Vertikalt streck på x = 
+ypts = [(0.1*magnitude+offset) max(y)*1.5];
+plot(xpts*t(x10r), ypts, '-'); // 10% rise
+plot(xpts*t(x10f), ypts, '-'); // 10% fall
+plot(xpts*t(x10r+5000), ypts, '-'); // second 10% rise
+ypts = [(0.9*magnitude+offset) max(y)*1.25];
+plot(xpts*t(x90r), ypts, '-'); // 90% rise
+
+// Generera horisontella linjer
+
+// Pulsen
+plot(t, y, "black");
+p = get("hdl");
+p = p.children;
+p.thickness = 3;
+
+// max och min horisontella
+hline = ones(1,length(t));
+plot(t,hline.*max(y), '--');
+plot(t,hline.*min(y), '--');
+plot(t,hline.*0, '-black');
+
+// 10 och 90% horizontella
+tshort = t(x10r-150:length(t))
+hline = ones(1,length(tshort));
+plot(tshort,hline.*y(x10r), '-');
+tshort = t(x10r-150:x90r)
+hline = ones(1,length(tshort));
+plot(tshort,hline.*y(x90r), '-');
+
+// titletxt = ['$y = k(e^{-\alpha t} - e^{-\beta t})$' ; strcat(['$k=', string(k), ', \alpha=', string(a), ', \beta=', string(b), '$']) ];
+
+//titletxt = '$u(t) = k(e^{-\alpha t} - e^{-\beta t})$';
+//title(titletxt , 'fontsize', 8);
+//xlabel('t (s)', 'fontsize', 7);
+//ylabel('U (V)', 'fontsize', 7, 'rotation', 0);
+
+a = get("current_axes");
+//a.axes_visible = "off";
+// Rita axlarna i 0
+//a.x_location = "origin";
+//a.y_location = "origin";
+
+
+// Bestäm viewport och ta bort inramning
+a.data_bounds = [min(t),0;max(t),200];
+a.box = "off";
+
+
+// Fula pilar (nästan) på axlarna
+//b = a.data_bounds
+//xstring(b(1),b(4),"↑")
+//set(gce(), "clip_state","off", "text_box_mode","centered", "font_size",4)
+//
+//xstring(b(2),b(3),"→")
+//set(gce(), "clip_state","off", "text_box_mode","centered", "font_size",4)
+
+f=get("current_figure")
+f.figure_size=f.figure_size*1.3  // Råkade bli lagom storlek
+

scilab/pulses/pulse3a.sce

@@ -0,0 +1,70 @@
+xdel(winsid())
+clear;
+
+t = [0:0.01:10];
+a = 1;
+b = 7;
+k = 1;
+
+magnitude = 100;
+offset = 20;
+
+y = k*(exp(-a*t) - exp(-b*t) );
+
+// Normalisera till 1 och multiplicera med magnituden
+y = y/max(y)*magnitude;
+
+ymax = max(y)*ones(1,length(y));
+
+// Create repetetive puses
+ylong=[];
+t=[];
+for i = [1:13]
+    if(modulo(i, 7) == 0 || modulo(i, 7) == 1) // Skip two pulses
+        ylong = [ylong zeros(1,length(y))];
+    else // The rest are pulses
+        ylong = [ylong y];
+    end
+end
+
+// Add offset voltage and create t axis that fits all pulses
+ylong = ylong*-1;
+ylong = ylong + offset;
+t = [1:length(ylong)];
+
+// Plot vertical lines
+xpts = [1 1];
+ypts = [0.3*magnitude 0]+offset;
+plot(xpts*1000, ypts, '-');
+plot(xpts*5000, ypts, '-');
+plot(xpts*8000, ypts, '-');
+ypts = [0.15*magnitude 0]+offset;
+plot(xpts*2000, ypts, '-');
+//plot(xpts*8.96, ypts, '--');
+
+// Plot horizontal lines
+plot(ones(1,length(ylong))*min(ylong), '--blue'); // min
+plot(ones(1,length(ylong))*max(ylong), '--blue'); // Max
+plot(ones(1,length(ylong))*0, '-black'); // Zero
+
+plot(t,ylong, 'black'); // Självaste pulsen
+p = get("hdl");
+p = p.children;
+p.thickness = 3;
+
+// titletxt = ['$y = k(e^{-\alpha t} - e^{-\beta t})$' ; strcat(['$k=', string(k), ', \alpha=', string(a), ', \beta=', string(b), '$']) ];
+
+titletxt = '$y = k(e^{-\alpha t} - e^{-\beta t})$';
+//title("Consecutive pulses", 'fontsize', 8);
+//xlabel('t (s)', 'fontsize', 7);
+//ylabel('U (V)', 'fontsize', 7, 'rotation', 0);
+
+a = get("current_axes");
+a.axes_visible(1) = "off"; // Turn off X-axxis
+a.data_bounds = [min(t), -magnitude; max(t),offset*3];
+a.box = "off";
+
+f=get("current_figure")
+f.figure_size=f.figure_size*1.3  // Råkade bli lagom storlek
+
+

scilab/pulses/pulse3b.sce

@@ -0,0 +1,69 @@
+xdel(winsid())
+clear;
+
+t = [0:0.01:10];
+a = 1;
+b = 7;
+k = 1;
+
+magnitude = 100;
+offset = 40;
+
+y = k*(exp(-a*t) - exp(-b*t) );
+
+// Normalisera till 1 och multiplicera med magnituden
+y = y/max(y)*magnitude;
+
+ymax = max(y)*ones(1,length(y));
+
+// Create repetetive puses
+ylong=[];
+t=[];
+for i = [1:13]
+    if(modulo(i, 7) == 0 || modulo(i, 7) == 1) // Skip two pulses
+        ylong = [ylong zeros(1,length(y))];
+    else // The rest are pulses
+        ylong = [ylong y];
+    end
+end
+
+// Add offset voltage and create t axis that fits all pulses
+ylong = ylong + offset;
+t = [1:length(ylong)];
+
+// Plot vertical lines
+xpts = [1 1];
+ypts = [-0.2*magnitude 0]+offset;
+plot(xpts*1000, ypts, '-');
+plot(xpts*5000, ypts, '-');
+plot(xpts*8000, ypts, '-');
+ypts = [-0.1*magnitude 0]+offset;
+plot(xpts*2000, ypts, '-');
+//plot(xpts*8.96, ypts, '--');
+
+// Plot horizontal lines
+plot(ones(1,length(ylong))*min(ylong), '--blue'); // min
+plot(ones(1,length(ylong))*max(ylong), '--blue'); // Max
+plot(ones(1,length(ylong))*0, '-black'); // Zero
+
+plot(t,ylong, 'black'); // Självaste pulsen
+p = get("hdl");
+p = p.children;
+p.thickness = 3;
+
+// titletxt = ['$y = k(e^{-\alpha t} - e^{-\beta t})$' ; strcat(['$k=', string(k), ', \alpha=', string(a), ', \beta=', string(b), '$']) ];
+
+titletxt = '$y = k(e^{-\alpha t} - e^{-\beta t})$';
+//title("Consecutive pulses", 'fontsize', 8);
+//xlabel('t (s)', 'fontsize', 7);
+//ylabel('U (V)', 'fontsize', 7, 'rotation', 0);
+
+a = get("current_axes");
+a.axes_visible(1) = "off"; // Turn off X-axxis
+a.data_bounds = [min(t), 0; max(t),1.05*(magnitude+offset)];
+a.box = "off";
+
+f=get("current_figure")
+f.figure_size=f.figure_size*1.3  // Råkade bli lagom storlek
+
+