|
@@ -49,7 +49,7 @@ A standard is developed and maintained by a Technical Committee, TC. The TC cons
|
|
|
|
|
|
|
|
The naming convention used for ISO standards is in the format \emph{number-part:year}, where the \emph{number} is the identifier to the unique ISO standard, \emph{part} denotes the part of the standard if it is divided into several parts and \emph{year} is the publishing year. For example; the name \emph{ISO~7637-2:2011} refers to part 2 of the ISO~7637 standard published in 2011, whilst \emph{ISO~7637-2:2004} would refer to an earlier version of the exact same document published in 2004.
|
|
The naming convention used for ISO standards is in the format \emph{number-part:year}, where the \emph{number} is the identifier to the unique ISO standard, \emph{part} denotes the part of the standard if it is divided into several parts and \emph{year} is the publishing year. For example; the name \emph{ISO~7637-2:2011} refers to part 2 of the ISO~7637 standard published in 2011, whilst \emph{ISO~7637-2:2004} would refer to an earlier version of the exact same document published in 2004.
|
|
|
|
|
|
|
|
-To get hold of a copy of a standard, one need to buy it from ISO store or from a national ISO member. \cite{site:iso_shopping_faqs}
|
|
|
|
|
|
|
+The ISO standards can be obtained from ISO's web store or from a national ISO member. \cite{site:iso_shopping_faqs}
|
|
|
|
|
|
|
|
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
|
|
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
|
|
|
\section{ISO~7637 and ISO~16750}
|
|
\section{ISO~7637 and ISO~16750}
|
|
@@ -57,7 +57,7 @@ To get hold of a copy of a standard, one need to buy it from ISO store or from a
|
|
|
\textbf{The ISO~7637 standard}, \emph{Road vehicles — Electrical disturbances from
|
|
\textbf{The ISO~7637 standard}, \emph{Road vehicles — Electrical disturbances from
|
|
|
conduction and coupling}, concerns the electrical environment in road vehicles. The standard consists of four parts, as of August 2019.
|
|
conduction and coupling}, concerns the electrical environment in road vehicles. The standard consists of four parts, as of August 2019.
|
|
|
|
|
|
|
|
-Part 1, \emph{Definitions and general considerations}, defines some abbreviations and technical terms that are used throughout the standard. It also intended use of the standard. \cite{iso_7637_1}
|
|
|
|
|
|
|
+Part 1, \emph{Definitions and general considerations}, define abbreviations and technical terms that are used throughout the standard. It also intended use of the standard. \cite{iso_7637_1}
|
|
|
|
|
|
|
|
Part 2, \emph{Electrical transient conduction along supply lines only}, defines the test procedures related to disturbances that are carried along the supply lines of a product. Both emission, disturbances created by the DUT, and immunity, the DUT's capability to withstand disturbances, are covered. This part defines the test pulses that are of interest for this project, and the verification of them. \cite{iso_7637_2}
|
|
Part 2, \emph{Electrical transient conduction along supply lines only}, defines the test procedures related to disturbances that are carried along the supply lines of a product. Both emission, disturbances created by the DUT, and immunity, the DUT's capability to withstand disturbances, are covered. This part defines the test pulses that are of interest for this project, and the verification of them. \cite{iso_7637_2}
|
|
|
|
|
|
|
@@ -73,20 +73,20 @@ The ISO~16750, \emph{Road vehicles -- Environmental conditions and testing for e
|
|
|
|
|
|
|
|
All test pulses defined in ISO~7637 and ISO~16750 are supposed to simulate events that can occur in a real vehicle's electrical environment, that equipment must be able to withstand. The properties of these test pulses are well defined, to allow for unified testing regardless of which test lab that performs the test. In the real world, however, the disturbances might of course differ from the test pulses since a real case environment is not controlled. \cite{iso_7637_2,iso_16750_2, comparison_iso_7637_real_world}
|
|
All test pulses defined in ISO~7637 and ISO~16750 are supposed to simulate events that can occur in a real vehicle's electrical environment, that equipment must be able to withstand. The properties of these test pulses are well defined, to allow for unified testing regardless of which test lab that performs the test. In the real world, however, the disturbances might of course differ from the test pulses since a real case environment is not controlled. \cite{iso_7637_2,iso_16750_2, comparison_iso_7637_real_world}
|
|
|
|
|
|
|
|
-The test pulses of interest defined in ISO~7637 are denoted \emph{Test pulse 1}, \emph{Test pulse 2a}, \emph{Test pulse 3a} and \emph{Test pulse 3b}. The test pulse of interest defined in ISO~16750 is denoted \emph{Load dump Test A}. There are more pulses and tests defined in these standards, but those are not in the scope of this project.
|
|
|
|
|
|
|
+The test pulses of interest defined in ISO~7637 are denoted \emph{test pulse 1}, \emph{test pulse 2a}, \emph{test pulse 3a} and \emph{test pulse 3b}. The test pulse of interest defined in ISO~16750 is denoted \emph{load dump test A}. There are more pulses and tests defined in these standards, but those are not in the scope of this project.
|
|
|
|
|
|
|
|
The general characteristics in common for all pulses are the DC voltage $U_A$, the surge voltage $U_s$, the rise time $t_r$, the pulse duration $t_d$ and the internal resistance $R_i$. The property \emph{internal resistance} is only in series with the generated pulse, not in series with the DC power source. For pulses that are supposed to be applied several times, $t_1$ usually denotes the time between the start of two consecutive pulses. The timings are illustrated in \autoref{fig:doubleexp}.
|
|
The general characteristics in common for all pulses are the DC voltage $U_A$, the surge voltage $U_s$, the rise time $t_r$, the pulse duration $t_d$ and the internal resistance $R_i$. The property \emph{internal resistance} is only in series with the generated pulse, not in series with the DC power source. For pulses that are supposed to be applied several times, $t_1$ usually denotes the time between the start of two consecutive pulses. The timings are illustrated in \autoref{fig:doubleexp}.
|
|
|
|
|
|
|
|
\begin{figure}[H]
|
|
\begin{figure}[H]
|
|
|
\centering
|
|
\centering
|
|
|
- \begin{subfigure}[t]{0.45\textwidth}
|
|
|
|
|
|
|
+ \begin{subfigure}[t]{0.6\textwidth}
|
|
|
\includegraphics[width=\textwidth]{doubleexpfunc}
|
|
\includegraphics[width=\textwidth]{doubleexpfunc}
|
|
|
\caption{The surge voltage $U_S$ is the puse maximum voltage disregarding the offset voltage $U_A$. The rise $t_r$ time is defined as the time elapsed from 0.1 to 0.9 times the surge voltage on the rising edge of the pulse. The duration $t_d$ is defined as the time from 0.1 times the maximum voltage on the rising edge, back to the same level of the falling edge.}
|
|
\caption{The surge voltage $U_S$ is the puse maximum voltage disregarding the offset voltage $U_A$. The rise $t_r$ time is defined as the time elapsed from 0.1 to 0.9 times the surge voltage on the rising edge of the pulse. The duration $t_d$ is defined as the time from 0.1 times the maximum voltage on the rising edge, back to the same level of the falling edge.}
|
|
|
\label{fig:doubleexp}
|
|
\label{fig:doubleexp}
|
|
|
\end{subfigure}\hfill
|
|
\end{subfigure}\hfill
|
|
|
\begin{subfigure}[t]{0.45\textwidth}
|
|
\begin{subfigure}[t]{0.45\textwidth}
|
|
|
\includegraphics[width=\textwidth]{doubleexpfuncrep}
|
|
\includegraphics[width=\textwidth]{doubleexpfuncrep}
|
|
|
- \caption{The repetition time is defined as the time between two adjacent rising edges.}
|
|
|
|
|
|
|
+ \caption{The repetition time $t_1$ is defined as the time between two adjacent rising edges.}
|
|
|
\label{fig:doubleexprep}
|
|
\label{fig:doubleexprep}
|
|
|
\end{subfigure}
|
|
\end{subfigure}
|
|
|
\caption{The common properties of the pulses, as defined by ISO~7637.}
|
|
\caption{The common properties of the pulses, as defined by ISO~7637.}
|
|
@@ -103,15 +103,14 @@ In the standard there are two additional timings associated to this pulse, $t_2$
|
|
|
\begin{figure}[H]
|
|
\begin{figure}[H]
|
|
|
%\captionsetup{width=.5\linewidth}
|
|
%\captionsetup{width=.5\linewidth}
|
|
|
\centering
|
|
\centering
|
|
|
- \includegraphics[width=\textwidth]{pulse1}
|
|
|
|
|
|
|
+ \includegraphics[width=0.6\textwidth]{pulse1}
|
|
|
\caption{Illustration of test pulse 1.}
|
|
\caption{Illustration of test pulse 1.}
|
|
|
\label{fig:pulse1}
|
|
\label{fig:pulse1}
|
|
|
\end{figure}
|
|
\end{figure}
|
|
|
-
|
|
|
|
|
\begin{table}[H]
|
|
\begin{table}[H]
|
|
|
\centering
|
|
\centering
|
|
|
\caption{Parameter values for pulse 1}
|
|
\caption{Parameter values for pulse 1}
|
|
|
- \begin{tabularx}{0.7\textwidth}{|X|c|c|}
|
|
|
|
|
|
|
+ \begin{tabularx}{0.45\textwidth}{|X|c|c|}
|
|
|
\hline
|
|
\hline
|
|
|
\textbf{Parameter} &\textbf{\SI{12}{\volt} system} &\textbf{\SI{24}{\volt} system} \\
|
|
\textbf{Parameter} &\textbf{\SI{12}{\volt} system} &\textbf{\SI{24}{\volt} system} \\
|
|
|
\hline
|
|
\hline
|
|
@@ -142,7 +141,7 @@ This pulse simulates the event of a load, parallel to the DUT, being disconnecte
|
|
|
\begin{figure}[H]
|
|
\begin{figure}[H]
|
|
|
%\captionsetup{width=.5\linewidth}
|
|
%\captionsetup{width=.5\linewidth}
|
|
|
\centering
|
|
\centering
|
|
|
- \includegraphics[width=\textwidth]{pulse2a}
|
|
|
|
|
|
|
+ \includegraphics[width=0.6\textwidth]{pulse2a}
|
|
|
\caption{Illustration of test pulse 2a.}
|
|
\caption{Illustration of test pulse 2a.}
|
|
|
\label{fig:pulse2a}
|
|
\label{fig:pulse2a}
|
|
|
\end{figure}
|
|
\end{figure}
|
|
@@ -172,19 +171,19 @@ This pulse simulates the event of a load, parallel to the DUT, being disconnecte
|
|
|
|
|
|
|
|
%%%%%%%%%%%%%%%%%%%
|
|
%%%%%%%%%%%%%%%%%%%
|
|
|
\subsection{Test pulse 3a and 3b}
|
|
\subsection{Test pulse 3a and 3b}
|
|
|
-Test pulse 3a and 3b simulates transients ``which occur as a result of the switching process'' as stated in the standard \cite{iso_7637_2}. The formulation is not very clear, but is interperted and explained by Frazier and Alles \cite{comparison_iso_7637_real_world} to be the result of a mechanical switch breaking an inductive load. These transients are very short, compared to the other pulses, and the repetition time is very short. The pulses are sent in bursts, grouping a number of pulses together and separating groups by a fixed time.
|
|
|
|
|
|
|
+Test pulse 3a and 3b simulate transients ``which occur as a result of the switching process'' as stated in the standard \cite{iso_7637_2}. The formulation is not very clear, but is interpreted and explained by Frazier and Alles \cite{comparison_iso_7637_real_world} to be the result of a mechanical switch breaking an inductive load. These transients are very short, compared to the other pulses, and the repetition time is very short. The pulses are sent in bursts, grouping a number of pulses together and separating groups by a fixed time.
|
|
|
|
|
|
|
|
These pulses contain high frequency components, up to 100~MHz, and special care must be taken when running tests with them as well as when verifying them.
|
|
These pulses contain high frequency components, up to 100~MHz, and special care must be taken when running tests with them as well as when verifying them.
|
|
|
|
|
|
|
|
|
|
|
|
|
\begin{figure}[H]
|
|
\begin{figure}[H]
|
|
|
\centering
|
|
\centering
|
|
|
- \begin{subfigure}[t]{0.45\textwidth}
|
|
|
|
|
|
|
+ \begin{subfigure}[t]{0.3\textwidth}
|
|
|
\includegraphics[width=\textwidth]{pulse3a}
|
|
\includegraphics[width=\textwidth]{pulse3a}
|
|
|
\caption{Pulse 3a}
|
|
\caption{Pulse 3a}
|
|
|
\label{fig:pulse3a}
|
|
\label{fig:pulse3a}
|
|
|
\end{subfigure}\hfill
|
|
\end{subfigure}\hfill
|
|
|
- \begin{subfigure}[t]{0.45\textwidth}
|
|
|
|
|
|
|
+ \begin{subfigure}[t]{0.3\textwidth}
|
|
|
\includegraphics[width=\textwidth]{pulse3b}
|
|
\includegraphics[width=\textwidth]{pulse3b}
|
|
|
\caption{Pulse 3b}
|
|
\caption{Pulse 3b}
|
|
|
\label{fig:pulse3b}
|
|
\label{fig:pulse3b}
|
|
@@ -224,16 +223,16 @@ These pulses contain high frequency components, up to 100~MHz, and special care
|
|
|
|
|
|
|
|
%%%%%%%%%%%%%%%%%%%
|
|
%%%%%%%%%%%%%%%%%%%
|
|
|
\subsection{Load dump Test A}
|
|
\subsection{Load dump Test A}
|
|
|
-The Load dump Test A simulates the event of disconnecting a battery that is charged by the vehicles alternator, the current that the alternator is driving will give rise to a long voltage transient.
|
|
|
|
|
|
|
+The load dump test A simulates the event of disconnecting a battery that is charged by the vehicles alternator, the current that the alternator is driving will give rise to a long voltage transient.
|
|
|
|
|
|
|
|
This pulse has the longest duration, $t_d$, of all the test pulses. It also has the lowest internal resistance. These properties makes it capable of transferring high energies into a low impedance DUT or dummy load.
|
|
This pulse has the longest duration, $t_d$, of all the test pulses. It also has the lowest internal resistance. These properties makes it capable of transferring high energies into a low impedance DUT or dummy load.
|
|
|
|
|
|
|
|
-Prior to 2011, the Load dump Test A was part of the ISO~7637-2 standard under the name \emph{Test pulse 5a}. The surge voltage $U_s$ was in the older standard, \mbox{ISO~7637-2:2004}, defined as the voltage between the DC offset voltage $U_A$ and the maximum voltage. In the newer standard, \mbox{ISO~16750-2:2012}, $U_s$ is defined as the absolute peak voltage. Only the former definition is used in this paper, $U_s = \hat{U} - U_A$.
|
|
|
|
|
|
|
+Prior to 2011, the load dump test A was part of the ISO~7637-2 standard under the name \emph{test pulse 5a}. The surge voltage $U_s$ was in the older standard, \mbox{ISO~7637-2:2004}, defined as the voltage between the DC offset voltage $U_A$ and the maximum voltage. In the newer standard, \mbox{ISO~16750-2:2012}, $U_s$ is defined as the absolute peak voltage. Only the former definition is used in this paper, $U_s = \hat{U} - U_A$.
|
|
|
|
|
|
|
|
\begin{figure}[H]
|
|
\begin{figure}[H]
|
|
|
%\captionsetup{width=.5\linewidth}
|
|
%\captionsetup{width=.5\linewidth}
|
|
|
\centering
|
|
\centering
|
|
|
- \includegraphics[width=\textwidth]{load dump a}
|
|
|
|
|
|
|
+ \includegraphics[width=0.6\textwidth]{load dump a}
|
|
|
\caption{Illustration of load dump Test A. Note the different definition of $U_S$ compared to the other pulses.}
|
|
\caption{Illustration of load dump Test A. Note the different definition of $U_S$ compared to the other pulses.}
|
|
|
\label{fig:loadDumpTestA}
|
|
\label{fig:loadDumpTestA}
|
|
|
\end{figure}
|
|
\end{figure}
|
|
@@ -263,7 +262,7 @@ Prior to 2011, the Load dump Test A was part of the ISO~7637-2 standard under th
|
|
|
|
|
|
|
|
%%%%%%%%%%%%%%%%%%%
|
|
%%%%%%%%%%%%%%%%%%%
|
|
|
\subsection{Application of test pulses}
|
|
\subsection{Application of test pulses}
|
|
|
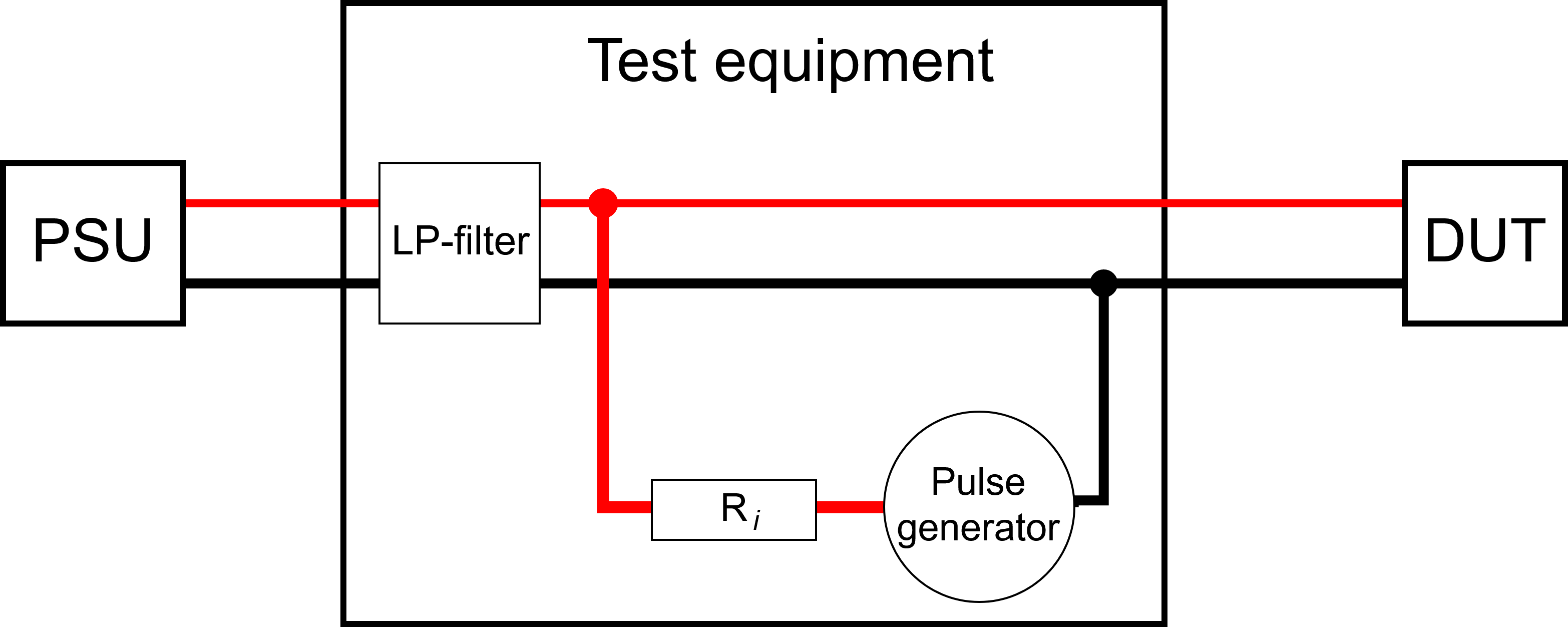
-During a test, the nominal voltage is first applied between the plus and minus terminal of the DUT's power supply input by the test equipment. Then a series of test pulses are applied between the same terminals. The pulses are repeated at specified intervals, $t_1$, as depicted in \autoref{fig:doubleexprep}.
|
|
|
|
|
|
|
+During a test, the nominal voltage is first applied between the plus and minus terminal of the DUT's power supply input by the test equipment. Then a series of test pulses are applied between the same terminals. The pulses are repeated at specified intervals, $t_1$, as depicted in \mbox{\autoref{fig:doubleexprep}}.
|
|
|
|
|
|
|
|
An example of how a test pulse can be applied by the test equipment is depicted in \autoref{fig:test_equipment_setup}.
|
|
An example of how a test pulse can be applied by the test equipment is depicted in \autoref{fig:test_equipment_setup}.
|
|
|
|
|
|
|
@@ -277,37 +276,38 @@ An example of how a test pulse can be applied by the test equipment is depicted
|
|
|
|
|
|
|
|
%%%%%%%%%%%%%%%%%%%
|
|
%%%%%%%%%%%%%%%%%%%
|
|
|
\subsection{Verification}
|
|
\subsection{Verification}
|
|
|
-The test pulses are to be verified before they are applied to the DUT. The voltage levels and the timings are to be measured both without any load, and with a matched load, $R_L$ = $R_i$, attached. The standard omits the rise time constraint when the load is attached, except for pulse 3a and 3b. \cite{iso_7637_2}
|
|
|
|
|
|
|
+\label{sec:theory:verification}
|
|
|
|
|
+The test pulses are to be verified before they are applied to the DUT. The voltage levels and the timings measured both without load, and with a dummy load $R_L$ which is matched to the generators internal resistance $R_i$. The standard omits the rise time constraint when the dummy load is attached, except for pulse 3a and 3b. \cite{iso_7637_2}
|
|
|
|
|
|
|
|
The verification is to be conducted with $U_A$ set to 0. There is, however, a proposal to set $U_A$ equal to the nominal voltage during the verification process, as the behaviour of the pulse generators has proven differ in this case \cite{iso_7637_5}. In this project $U_A = 0$ will be used.
|
|
The verification is to be conducted with $U_A$ set to 0. There is, however, a proposal to set $U_A$ equal to the nominal voltage during the verification process, as the behaviour of the pulse generators has proven differ in this case \cite{iso_7637_5}. In this project $U_A = 0$ will be used.
|
|
|
|
|
|
|
|
The limits, and tolerances, for the pulses are summarised in \autoref{tab:verification-list}. The matched loads are to be within 1\% of the nominal value.
|
|
The limits, and tolerances, for the pulses are summarised in \autoref{tab:verification-list}. The matched loads are to be within 1\% of the nominal value.
|
|
|
|
|
|
|
|
-The instruments used for measuring the pulses must have at least \SI{400}{\mega\hertz}, since pulse 3a and 3b contains frequency components of up to \SI{200}{\mega\hertz}.
|
|
|
|
|
|
|
+The instruments used for measuring the pulses must have at least \SI{400}{\mega\hertz}, since pulse 3a and 3b contains frequency components of up to \SI{200}{\mega\hertz}. The measurement in open state for pulse 3a and 3b is a compromise, since a passive attenuator that does not load the input would be impossible to make, and was made as a 1000-ohm attenuator instead. This is how a similar generator is tested in another standard, the burst test \todo[Ta reda på hur det kommer sig att vi kör med 1k istället för oändligt].
|
|
|
|
|
|
|
|
\begin{table}[H]
|
|
\begin{table}[H]
|
|
|
- \caption{These are all of the verifications that needs to be made before each use of the equipment, along with the limits for each case.}
|
|
|
|
|
|
|
+ \caption{These are all of the verifications that needs to be made before each use of the equipment, along with the limits specified in ISO~7637-2.}
|
|
|
\begin{adjustbox}{width=\columnwidth,center}
|
|
\begin{adjustbox}{width=\columnwidth,center}
|
|
|
%\centering
|
|
%\centering
|
|
|
\begin{tabular}{|l|r|r|r|r|}
|
|
\begin{tabular}{|l|r|r|r|r|}
|
|
|
\hline
|
|
\hline
|
|
|
& & \multicolumn{3}{c|}{Limits}\\
|
|
& & \multicolumn{3}{c|}{Limits}\\
|
|
|
- Pulse & Match resistor & $U_S$ & $t_d$ & $t_r$ \\
|
|
|
|
|
- \hline
|
|
|
|
|
- Pulse 1, 12 V, Open & & \SIrange{-110}{ -90}{\volt} & \SIrange{1.6}{2.4}{\milli\second} & \SIrange{0.5}{ 1}{\micro\second} \\
|
|
|
|
|
- Pulse 1, 12 V, Matched & 10 \si{\ohm} & \SIrange{-110}{ -90}{\volt} & \SIrange{1.6}{2.4}{\milli\second} & \SIrange{0.5}{ 1}{\micro\second} \\
|
|
|
|
|
- Pulse 1, 24 V, Open & & \SIrange{-660}{-540}{\volt} & \SIrange{0.8}{1.2}{\milli\second} & \SIrange{1.5}{ 3}{\micro\second} \\
|
|
|
|
|
- Pulse 1, 24 V, Matched & 50 \si{\ohm} & \SIrange{-660}{-540}{\volt} & \SIrange{0.8}{1.2}{\milli\second} & \SIrange{1.5}{ 3}{\micro\second} \\
|
|
|
|
|
- Pulse 2a, Open & & \SIrange{67.5}{82.5}{\volt} & \SIrange{ 40}{ 60}{\micro\second} & \SIrange{0.5}{ 1}{\micro\second} \\
|
|
|
|
|
- Pulse 2a, Matched & 2 \si{\ohm} & \SIrange{67.5}{82.5}{\volt} & \SIrange{ 40}{ 60}{\micro\second} & \SIrange{0.5}{ 1}{\micro\second} \\
|
|
|
|
|
- Pulse 3a, Open (1k) & & \SIrange{-220}{-180}{\volt} & \SIrange{105}{195}{\nano\second} & \SIrange{3.5}{6.5}{\nano\second} \\
|
|
|
|
|
- Pulse 3a, Match & 50 \si{\ohm} & \SIrange{-120}{ -80}{\volt} & \SIrange{105}{195}{\nano\second} & \SIrange{3.5}{6.5}{\nano\second} \\
|
|
|
|
|
- Pulse 3b, Open (1k) & & \SIrange{ 180}{ 220}{\volt} & \SIrange{105}{195}{\nano\second} & \SIrange{3.5}{6.5}{\nano\second} \\
|
|
|
|
|
- Pulse 3b, Match & 50 \si{\ohm} & \SIrange{ 80}{ 120}{\volt} & \SIrange{105}{195}{\nano\second} & \SIrange{3.5}{6.5}{\nano\second} \\
|
|
|
|
|
- Load dump A, 12 V, Open & & \SIrange{ 90}{ 110}{\volt} & \SIrange{320}{480}{\milli\second} & \SIrange{ 5}{ 10}{\milli\second} \\
|
|
|
|
|
- Load dump A, 12 V, Matched & 2 \si{\ohm} & \SIrange{ 90}{ 110}{\volt} & \SIrange{320}{480}{\milli\second} & \SIrange{ 5}{ 10}{\milli\second} \\
|
|
|
|
|
- Load dump A, 24 V, Open & & \SIrange{ 180}{ 220}{\volt} & \SIrange{280}{420}{\milli\second} & \SIrange{ 5}{ 10}{\milli\second} \\
|
|
|
|
|
- Load dump A, 24 V, Matched & 2 \si{\ohm} & \SIrange{ 180}{ 220}{\volt} & \SIrange{280}{420}{\milli\second} & \SIrange{ 5}{ 10}{\milli\second} \\
|
|
|
|
|
|
|
+ Test pulse & Match resistor & $U_S$ & $t_d$ & $t_r$ \\
|
|
|
|
|
+ \hline
|
|
|
|
|
+ Test pulse 1, 12 V, Open & & \SIrange{-110}{ -90}{\volt} & \SIrange{1.6}{2.4}{\milli\second} & \SIrange{0.5}{ 1}{\micro\second} \\
|
|
|
|
|
+ Test pulse 1, 12 V, Matched & 10 \si{\ohm} & \SIrange{ -60}{ -40}{\volt} & \SIrange{1.6}{2.4}{\milli\second} & N/A \\
|
|
|
|
|
+ Test pulse 1, 24 V, Open & & \SIrange{-660}{-540}{\volt} & \SIrange{0.8}{1.2}{\milli\second} & \SIrange{1.5}{ 3}{\micro\second} \\
|
|
|
|
|
+ Test pulse 1, 24 V, Matched & 50 \si{\ohm} & \SIrange{-360}{-240}{\volt} & \SIrange{0.8}{1.2}{\milli\second} & N/A \\
|
|
|
|
|
+ Test pulse 2a, Open & & \SIrange{67.5}{82.5}{\volt} & \SIrange{ 40}{ 60}{\micro\second} & \SIrange{0.5}{ 1}{\micro\second} \\
|
|
|
|
|
+ Test pulse 2a, Matched & 2 \si{\ohm} & \SIrange{ 45}{ 30}{\volt} & \SIrange{ 40}{ 60}{\micro\second} & \SIrange{0.5}{ 1}{\micro\second} \\
|
|
|
|
|
+ Test pulse 3a, Open (1k) & & \SIrange{-220}{-180}{\volt} & \SIrange{105}{195}{\nano\second} & \SIrange{3.5}{6.5}{\nano\second} \\
|
|
|
|
|
+ Test pulse 3a, Match & 50 \si{\ohm} & \SIrange{-120}{ -80}{\volt} & \SIrange{105}{195}{\nano\second} & \SIrange{3.5}{6.5}{\nano\second} \\
|
|
|
|
|
+ Test pulse 3b, Open (1k) & & \SIrange{ 180}{ 220}{\volt} & \SIrange{105}{195}{\nano\second} & \SIrange{3.5}{6.5}{\nano\second} \\
|
|
|
|
|
+ Test pulse 3b, Match & 50 \si{\ohm} & \SIrange{ 80}{ 120}{\volt} & \SIrange{105}{195}{\nano\second} & \SIrange{3.5}{6.5}{\nano\second} \\
|
|
|
|
|
+ Load dump test A, 12 V, Open & & \SIrange{ 90}{ 110}{\volt} & \SIrange{320}{480}{\milli\second} & \SIrange{ 5}{ 10}{\milli\second} \\
|
|
|
|
|
+ Load dump test A, 12 V, Matched & 2 \si{\ohm} & \SIrange{ 40}{ 60}{\volt} & \SIrange{160}{240}{\milli\second} & N/A \\
|
|
|
|
|
+ Load dump test A, 24 V, Open & & \SIrange{ 180}{ 220}{\volt} & \SIrange{280}{420}{\milli\second} & \SIrange{ 5}{ 10}{\milli\second} \\
|
|
|
|
|
+ Load dump test A, 24 V, Matched & 2 \si{\ohm} & \SIrange{ 80}{ 120}{\volt} & \SIrange{140}{210}{\milli\second} & N/A \\
|
|
|
\hline
|
|
\hline
|
|
|
\end{tabular}
|
|
\end{tabular}
|
|
|
\end{adjustbox}
|
|
\end{adjustbox}
|
|
@@ -318,9 +318,10 @@ The instruments used for measuring the pulses must have at least \SI{400}{\mega\
|
|
|
\section{Resistors at high frequencies}
|
|
\section{Resistors at high frequencies}
|
|
|
\label{sec:theory:resistors_at_high_frequencies}
|
|
\label{sec:theory:resistors_at_high_frequencies}
|
|
|
|
|
|
|
|
-When working with resistors at high frequencies, one must consider the parasitc properties of the resistor. Vishay presents a model which consists of the resistance $R$, internal inductance $L$, internal capacitance $C$, external lead inductance $L_C$ and external ground capacitance $C_G$. Since the external ground capacitance is very small in comparison to the other parasitics, it has been neglected in this thesis. The model used for the simulations is depicted in \autoref{fig:nonIdealResistor}, with the values $L = \SI{0.1}{\nano\henry}$, $C = \SI{1}{\pico\farad}$ and $L_C = \SI{1}{\nano\henry}$. This is a bit higher than the values in Vishays paper, but those are also for smaller packages. \cite{vishay_hf_resistor} An approximation of the combined inductance of more than \SI{1}{\nano\henry} for the 1206 package is also in line with the values in a technical information note from AVX for capacitors, the package lead inductance should be similar for capacitors and resistors\cite{avx_cap_parasitic}.
|
|
|
|
|
|
|
+When working with resistors at high frequencies, one must consider the parasitc properties of the resistor. Vishay presents a model which consists of the resistance $R$, internal inductance $L$, internal capacitance $C$, external lead inductance $L_C$ and external ground capacitance $C_G$. \cite{vishay_hf_resistor} Since the external ground capacitance is very small in comparison to the other parasitics, it has been neglected in this thesis. The model used for the simulations is depicted in \autoref{fig:nonIdealResistor}, with the values $L = \SI{0.1}{\nano\henry}$, $C = \SI{1}{\pico\farad}$ and $L_C = \SI{1}{\nano\henry}$. This is a bit higher than the values in Vishays paper, but those are also for smaller packages. An approximation of the combined inductance of more than \SI{1}{\nano\henry} for the 1206 SMD package is also in line with the values in a technical information note from AVX for capacitors, the package lead inductance should be similar for capacitors and resistors. \cite{avx_cap_parasitic}
|
|
|
|
|
|
|
|
\begin{figure}[H]
|
|
\begin{figure}[H]
|
|
|
|
|
+ \centering
|
|
|
\includegraphics[width=0.5\textwidth]{nonIdealResistor}
|
|
\includegraphics[width=0.5\textwidth]{nonIdealResistor}
|
|
|
\caption{At high frequencies a resistors parasitic inductance and capacitance will affect the behavior of the circuit. This is the model used in this thesis when simulating circuits.}
|
|
\caption{At high frequencies a resistors parasitic inductance and capacitance will affect the behavior of the circuit. This is the model used in this thesis when simulating circuits.}
|
|
|
\label{fig:nonIdealResistor}
|
|
\label{fig:nonIdealResistor}
|
|
@@ -333,10 +334,11 @@ There are several measurement methods needed during the project. To verify the t
|
|
|
%%%%%%%%%%%%%%%%%%%
|
|
%%%%%%%%%%%%%%%%%%%
|
|
|
\subsection{Resistance}
|
|
\subsection{Resistance}
|
|
|
\label{sec:measurement:resistance}
|
|
\label{sec:measurement:resistance}
|
|
|
-To measure resistance, a current is fed through the resistor and the resulting voltage is measured to calculate the resistance using ohms law. This is typically carried out using a multimeter and two probe wires connecting to each terminal of the resistor. When measuring very low valued resistors, however, the resistance in the probe wires can be significant in relation to the resistor measured and will affect the accuracy. One way of overcoming this is to perform a 4-wire measurement using a so called \emph{Kelvin connection}. In this method the current that is fed through the resistor using one pair of wire, and the resulting voltage is measured at the desired point using another pair according to \autoref{fig:kelvin_measurement}.\cite{theCircuitDesignersCompanion}
|
|
|
|
|
|
|
+Resistance can be determined by applying a known voltage and measure the resulting current or, the other way around, applying a known current and measure the resulting voltage. The resistance is then calculated from these values using Ohm's law. This is typically done using a multimeter and two probe wires to connect each terminal of the resistor. When measuring very low valued resistors, however, the resistance in the probe wires can be significant in relation to the resistor measured and will affect the accuracy. One way of overcoming this is to perform a 4-wire measurement using a so called \emph{Kelvin connection}. In this method the current that is fed through the resistor using one pair of wire, and the resulting voltage is measured at the desired point using another pair according to \autoref{fig:kelvin_measurement}.\cite{theCircuitDesignersCompanion}
|
|
|
|
|
|
|
|
\begin{figure}[H]
|
|
\begin{figure}[H]
|
|
|
%\captionsetup{width=.5\linewidth}
|
|
%\captionsetup{width=.5\linewidth}
|
|
|
|
|
+ \centering
|
|
|
\includegraphics[width=0.5\textwidth]{kelvin_measurement}
|
|
\includegraphics[width=0.5\textwidth]{kelvin_measurement}
|
|
|
\caption{When measuring a low value resistor, the \emph{Kelvin connection} can be used to determine the resistance at the point where the voltmeter is connected without the resistance in the probe leads affecting the result.}
|
|
\caption{When measuring a low value resistor, the \emph{Kelvin connection} can be used to determine the resistance at the point where the voltmeter is connected without the resistance in the probe leads affecting the result.}
|
|
|
\label{fig:kelvin_measurement}
|
|
\label{fig:kelvin_measurement}
|
|
@@ -344,7 +346,7 @@ To measure resistance, a current is fed through the resistor and the resulting v
|
|
|
|
|
|
|
|
%%%%%%%%%%%%%%%%%%%
|
|
%%%%%%%%%%%%%%%%%%%
|
|
|
\subsection{Oscilloscopes, bandwidth, rise time and probes}
|
|
\subsection{Oscilloscopes, bandwidth, rise time and probes}
|
|
|
-When using an oscilloscope to measure voltage over time, there are several limiting factors to how fast signals one can measure. The oscilloscope itself has a specified bandwidth, as do the probe and any attenuators used. All of these combined determine how short rise times that can be measured accurately. The rise time of the measured will be affected by these properties and the rise time displayed on the oscilloscope screen will be approximately according to \autoref{equ:riseComposite}, where $T_N$ is the \SIrange{10}{90}{\percent} rise time limit for each part in the chain. \cite{highSpeedDigitalDesign}
|
|
|
|
|
|
|
+When using an oscilloscope to measure voltage over time, there are several limiting factors to how fast signals one can measure. The oscilloscope itself has a specified bandwidth, as do the probe and any attenuators used. All of these combined determine how short rise times that can be measured accurately. The rise time of the measured signal will be affected by these properties and the rise time displayed on the oscilloscope screen will be approximately according to \autoref{equ:riseComposite}, where $T_N$ is the \SIrange{10}{90}{\percent} rise time limit for each part in the chain. \cite{highSpeedDigitalDesign}
|
|
|
|
|
|
|
|
\begin{equation}
|
|
\begin{equation}
|
|
|
\label{equ:riseComposite}
|
|
\label{equ:riseComposite}
|
|
@@ -355,7 +357,7 @@ Since \autoref{equ:riseComposite} is based on the rise time limitation but the s
|
|
|
|
|
|
|
|
\begin{equation}
|
|
\begin{equation}
|
|
|
\label{equ:bwToRise}
|
|
\label{equ:bwToRise}
|
|
|
-T_{10-90} = \frac{0.338}{F_{ \SI{3}{\deci\bel}}}
|
|
|
|
|
|
|
+T_{10-90} = \frac{0.338}{F_{ \SI{3}{\deci\bel}}}\si{\second}
|
|
|
\end{equation}
|
|
\end{equation}
|
|
|
|
|
|
|
|
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
|
|
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
|
|
@@ -364,25 +366,25 @@ The data points from the measurement must be processed and evaluated to determin
|
|
|
|
|
|
|
|
%%%%%%%%%%%%%%%%%%%
|
|
%%%%%%%%%%%%%%%%%%%
|
|
|
\subsection{Mathematical description}
|
|
\subsection{Mathematical description}
|
|
|
-All of the test pulses applied to the vehicle equipment can individually be described mathematically by variations of the double exponential function shown in \autoref{eq:doubleexp}. The properties of interest, the ones which are specified in the standards, are the surge voltage $ U_s $, the rise time $ t_r $, the duration $ t_d $ and the repetition time $ t_1 $. \cite{iso_7637_2}
|
|
|
|
|
|
|
+All test pulses applied to the vehicle equipment can individually be described mathematically by variations of the double exponential function shown in \autoref{eq:doubleexp}. The properties of interest, the ones which are specified in the standards, are the surge voltage $ U_s $, the rise time $ t_r $, the duration $ t_d $ and the repetition time $ t_1 $. \cite{iso_7637_2}
|
|
|
|
|
|
|
|
\begin{equation}
|
|
\begin{equation}
|
|
|
u(t)=k(e^{\alpha t} - e^{\beta t}) + U_{A}
|
|
u(t)=k(e^{\alpha t} - e^{\beta t}) + U_{A}
|
|
|
\label{eq:doubleexp}
|
|
\label{eq:doubleexp}
|
|
|
\end{equation}
|
|
\end{equation}
|
|
|
|
|
|
|
|
-It is not in the scope of this report to actually fit this function to the measured pulse, and further analyze it.
|
|
|
|
|
|
|
+It is not in the scope of this report to actually fit this function to the measured pulses, and further analyze it.
|
|
|
|
|
|
|
|
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
|
|
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
|
|
|
\section{Instrumentation and control}
|
|
\section{Instrumentation and control}
|
|
|
-The following chapter describes the different instruments that were used, and their control interfaces.
|
|
|
|
|
|
|
+The following chapter describes the different instruments that were used, and their control interfaces. Some of these are equipped with GPIB, General Purpose Interface Bus, which is a parallel bus used for controlling instruments.
|
|
|
|
|
|
|
|
%%%%%%%%%%%%%%%%%%%
|
|
%%%%%%%%%%%%%%%%%%%
|
|
|
\subsection{Tektronix TDS7104 Oscilloscope}
|
|
\subsection{Tektronix TDS7104 Oscilloscope}
|
|
|
-The oscilloscope available for this project is a Tektronix TDS7104, with specifications as seen in \autoref{tab:tds7104}. It has GPIB interface and TekVISA GPIB, an API for sending GPIB commands over ethernet, available for remote control. \footnote{\url{https://www.tek.com/datasheet/tds7000-series}}
|
|
|
|
|
|
|
+The oscilloscope available for this project is a Tektronix TDS7104\footnote{\url{https://www.tek.com/datasheet/tds7000-series}}, with specifications as seen in \autoref{tab:tds7104}. It has GPIB interface and TekVISA GPIB, an API for sending GPIB commands over ethernet, available for remote control.
|
|
|
|
|
|
|
|
\begin{table}[H]
|
|
\begin{table}[H]
|
|
|
- \caption{Specs of the Tektronix TDS7104}
|
|
|
|
|
|
|
+ \caption{A selection of the specifications for the Tektronix TDS7104}
|
|
|
\begin{adjustbox}{center}
|
|
\begin{adjustbox}{center}
|
|
|
%\centering
|
|
%\centering
|
|
|
\begin{tabular}{|l|r|}
|
|
\begin{tabular}{|l|r|}
|
|
@@ -393,8 +395,6 @@ The oscilloscope available for this project is a Tektronix TDS7104, with specifi
|
|
|
\hline
|
|
\hline
|
|
|
Channels & $4$ \\
|
|
Channels & $4$ \\
|
|
|
\hline
|
|
\hline
|
|
|
- Interfaces & GPIB, TekVISA \\
|
|
|
|
|
- \hline
|
|
|
|
|
\end{tabular}
|
|
\end{tabular}
|
|
|
\end{adjustbox}
|
|
\end{adjustbox}
|
|
|
\label{tab:tds7104}
|
|
\label{tab:tds7104}
|
|
@@ -407,7 +407,7 @@ The oscilloscope available for this project is a Tektronix TDS7104, with specifi
|
|
|
|
|
|
|
|
%%%%%%%%%%%%%%%%%%%
|
|
%%%%%%%%%%%%%%%%%%%
|
|
|
\subsection{EM Test MPG 200 Micropulse generator}
|
|
\subsection{EM Test MPG 200 Micropulse generator}
|
|
|
-The MPG~200 is used to generate \emph{Test pulse 1} and \emph{2a}. MPG is an abbreviation for \emph{MicroPulse Generator}. The instrument is designed to generate test pulses according to the older ISO~7637-2:1990 version, but the parameters can be adjusted to comply with the new ISO~7637:1990 standard. The adjustable parameter ranges are shown in \autoref{tab:mpg200_specs}. The instrumentation panels can be seen in \autoref{fig:mpg200}.
|
|
|
|
|
|
|
+The MPG~200 is used to generate \emph{test pulse 1} and \emph{2a}. MPG is an abbreviation for \emph{MicroPulse Generator}. The instrument is designed to generate test pulses according to the older ISO~7637-2:1990 version, but the parameters can be adjusted to comply with the new ISO~7637:1990 standard. The adjustable parameter ranges are shown in \autoref{tab:mpg200_specs}. The instrumentation panels can be seen in \autoref{fig:mpg200}. It can be controlled via a GPIB interface.
|
|
|
|
|
|
|
|
\begin{table}[H]
|
|
\begin{table}[H]
|
|
|
\caption{Adjustable parameters in the MPG 200}
|
|
\caption{Adjustable parameters in the MPG 200}
|
|
@@ -415,10 +415,10 @@ The MPG~200 is used to generate \emph{Test pulse 1} and \emph{2a}. MPG is an abb
|
|
|
%\centering
|
|
%\centering
|
|
|
\begin{tabular}{|l|r|}
|
|
\begin{tabular}{|l|r|}
|
|
|
\hline
|
|
\hline
|
|
|
- Parameter & Range \\
|
|
|
|
|
|
|
+ Parameter & Available settings \\
|
|
|
\hline
|
|
\hline
|
|
|
$U_S$ & \SIrange{20}{600}{\volt} \\
|
|
$U_S$ & \SIrange{20}{600}{\volt} \\
|
|
|
- $U_S$ polarity & +, - \\
|
|
|
|
|
|
|
+ $U_S$ polarity & $+$, $-$ \\
|
|
|
$R_s$ & \SIlist{2;4;10;20;30;50}{\ohm} \\
|
|
$R_s$ & \SIlist{2;4;10;20;30;50}{\ohm} \\
|
|
|
$t_1$ & \SIrange{0.2}{99.0}{\second} \\
|
|
$t_1$ & \SIrange{0.2}{99.0}{\second} \\
|
|
|
$t_2$ & \SIrange{0}{10}{\second} \\
|
|
$t_2$ & \SIrange{0}{10}{\second} \\
|
|
@@ -448,7 +448,7 @@ The MPG~200 is used to generate \emph{Test pulse 1} and \emph{2a}. MPG is an abb
|
|
|
|
|
|
|
|
%%%%%%%%%%%%%%%%%%%
|
|
%%%%%%%%%%%%%%%%%%%
|
|
|
\subsection{EM Test EFT 200 Burst generator}
|
|
\subsection{EM Test EFT 200 Burst generator}
|
|
|
-The EFT~200 is used to generate \emph{Test pulse 3a} and \emph{3b}. EFT is an abbreviation for \emph{Electrical Fast Transient}. The instrument is designed to generate test pulses according to the older ISO~7637-2:1990 version, but the parameters can be adjusted to comply with the new ISO~7637:1990 standard. The adjustable parameter ranges are shown in \autoref{tab:eft200_specs}. The instrumentation panels can be seen in \autoref{fig:eft200}.
|
|
|
|
|
|
|
+The EFT~200 is used to generate \emph{test pulse 3a} and \emph{3b}. EFT is an abbreviation for \emph{Electrical Fast Transient}. The instrument is designed to generate test pulses according to the older ISO~7637-2:1990 version, but the parameters can be adjusted to comply with the new ISO~7637:1990 standard. The adjustable parameter ranges are shown in \autoref{tab:eft200_specs}. The instrumentation panels can be seen in \autoref{fig:eft200}. It can be controlled via a GPIB interface.
|
|
|
|
|
|
|
|
\begin{table}[H]
|
|
\begin{table}[H]
|
|
|
\caption{Adjustable parameters in the EFT 200}
|
|
\caption{Adjustable parameters in the EFT 200}
|
|
@@ -456,11 +456,11 @@ The EFT~200 is used to generate \emph{Test pulse 3a} and \emph{3b}. EFT is an ab
|
|
|
%\centering
|
|
%\centering
|
|
|
\begin{tabular}{|l|r|}
|
|
\begin{tabular}{|l|r|}
|
|
|
\hline
|
|
\hline
|
|
|
- Parameter & Range \\
|
|
|
|
|
|
|
+ Parameter & Available settings \\
|
|
|
\hline
|
|
\hline
|
|
|
$U_S$ & \SIrange{25}{1500}{\volt} \\
|
|
$U_S$ & \SIrange{25}{1500}{\volt} \\
|
|
|
- $U_S$ polarity & +, - \\
|
|
|
|
|
- Coupling & any combination of +, - and GND \\
|
|
|
|
|
|
|
+ $U_S$ polarity & $+$, $-$ \\
|
|
|
|
|
+ Coupling & any combination of $+$, $-$ and GND \\
|
|
|
\hline
|
|
\hline
|
|
|
\end{tabular}
|
|
\end{tabular}
|
|
|
\end{adjustbox}
|
|
\end{adjustbox}
|
|
@@ -486,8 +486,8 @@ The EFT~200 is used to generate \emph{Test pulse 3a} and \emph{3b}. EFT is an ab
|
|
|
\end{figure}
|
|
\end{figure}
|
|
|
|
|
|
|
|
%%%%%%%%%%%%%%%%%%%
|
|
%%%%%%%%%%%%%%%%%%%
|
|
|
-\subsection{EM Test LD 200 Load dump}
|
|
|
|
|
-The LD~200 is used to generate \emph{Load dump Test A}. LD is an abbreviation for \emph{Load Dump}. The instrument is designed to generate test pulses according to the older ISO~7637-2:1990 version, but the parameters can be adjusted to comply with the new ISO~16750:2012 standard. The adjustable parameter ranges are shown in \autoref{tab:ld200_specs}. The instrumentation panels can be seen in \autoref{fig:ld200}.
|
|
|
|
|
|
|
+\subsection{EM Test LD 200 Load dump generator}
|
|
|
|
|
+The LD~200 is used to generate \emph{load dump test A}. LD is an abbreviation for \emph{load dump}. The instrument is designed to generate test pulses according to the older ISO~7637-2:1990 version, but the parameters can be adjusted to comply with the new ISO~16750:2012 standard. The adjustable parameter ranges are shown in \autoref{tab:ld200_specs}. The instrumentation panels can be seen in \autoref{fig:ld200}. It can be controlled via a GPIB interface.
|
|
|
|
|
|
|
|
\begin{table}[H]
|
|
\begin{table}[H]
|
|
|
\caption{Adjustable parameters in the LD 200}
|
|
\caption{Adjustable parameters in the LD 200}
|
|
@@ -495,7 +495,7 @@ The LD~200 is used to generate \emph{Load dump Test A}. LD is an abbreviation fo
|
|
|
%\centering
|
|
%\centering
|
|
|
\begin{tabular}{|l|r|}
|
|
\begin{tabular}{|l|r|}
|
|
|
\hline
|
|
\hline
|
|
|
- Parameter & Range \\
|
|
|
|
|
|
|
+ Parameter & Available settings \\
|
|
|
\hline
|
|
\hline
|
|
|
$U_S$ & \SIrange{20}{200}{\volt} \\
|
|
$U_S$ & \SIrange{20}{200}{\volt} \\
|
|
|
$R_s$ & \SIlist{0.5;1;2;10}{\ohm} \\
|
|
$R_s$ & \SIlist{0.5;1;2;10}{\ohm} \\
|
|
@@ -520,16 +520,17 @@ The LD~200 is used to generate \emph{Load dump Test A}. LD is an abbreviation fo
|
|
|
\caption{Back.}
|
|
\caption{Back.}
|
|
|
\label{fig:ld200-back}
|
|
\label{fig:ld200-back}
|
|
|
\end{subfigure}
|
|
\end{subfigure}
|
|
|
- \caption{The LD~200 is used to generate load dump test a.}
|
|
|
|
|
|
|
+ \caption{The LD~200 is used to generate load dump test A.}
|
|
|
\label{fig:ld200}
|
|
\label{fig:ld200}
|
|
|
\end{figure}
|
|
\end{figure}
|
|
|
|
|
|
|
|
%%%%%%%%%%%%%%%%%%%
|
|
%%%%%%%%%%%%%%%%%%%
|
|
|
\subsection{EM Test CNA 200 Coupling Network}
|
|
\subsection{EM Test CNA 200 Coupling Network}
|
|
|
-The SNA~200 is a coupling network used to multiplex the pulse generators outputs. It contains several relays to select the appropriate generator output. The SNA~200 has one interface for each pulse generator, but no interface for a computer. It is automatically controlled by the pulse generators. This allows the DUT to be connected only to the CNA~200 and not to each individual pulse generator. \autoref{fig:test_setup_cna_dut} shows the connections between the instruments in this setup. There is also a coaxial connection for calibration of pulse 3a and pulse 3b on the front panel. The instrumentation panels can be seen in \autoref{fig:cna200}.
|
|
|
|
|
|
|
+The SNA~200 is a coupling network used to multiplex the pulse generators outputs. It contains several relays to select the appropriate generator output. The SNA~200 has one interface for each pulse generator, but no interface for a computer. It is automatically controlled by the pulse generators. This allows the DUT to be connected only to the CNA~200 and not to each individual pulse generator. \autoref{fig:test_setup_cna_dut} shows the connections between the instruments in this setup. There is also a coaxial connection for calibration of pulse 3a and pulse 3b on the front panel. The instrumentation panels can be seen in \autoref{fig:cna200}. The CNA~200 have no controls or manual settings since it is controlled by the test generators that are attached to it via DSUB-connectors.
|
|
|
|
|
|
|
|
\begin{figure}[H]
|
|
\begin{figure}[H]
|
|
|
%\captionsetup{width=.5\linewidth}
|
|
%\captionsetup{width=.5\linewidth}
|
|
|
|
|
+ \centering
|
|
|
\includegraphics[width=0.5\textwidth]{test setup pulse injection}
|
|
\includegraphics[width=0.5\textwidth]{test setup pulse injection}
|
|
|
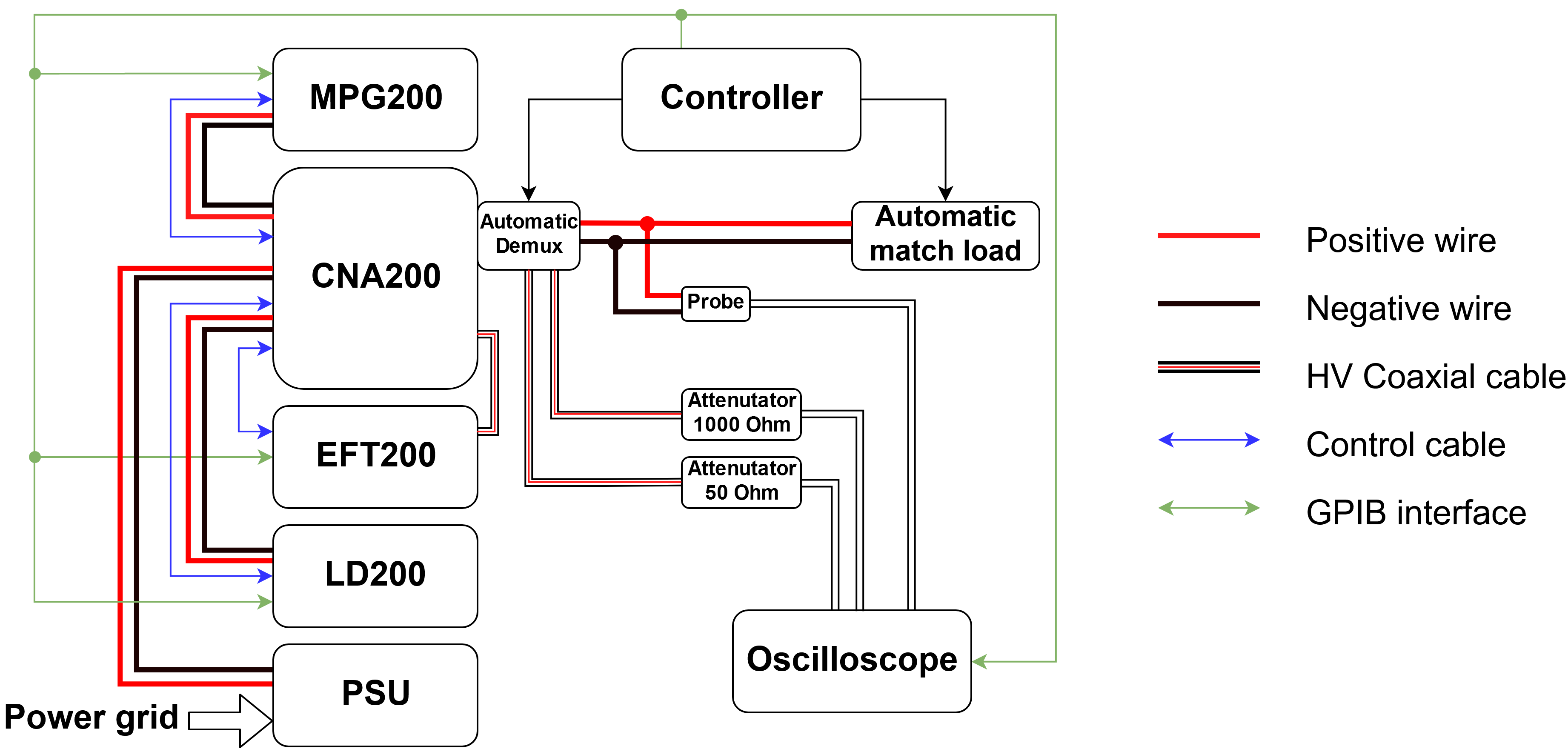
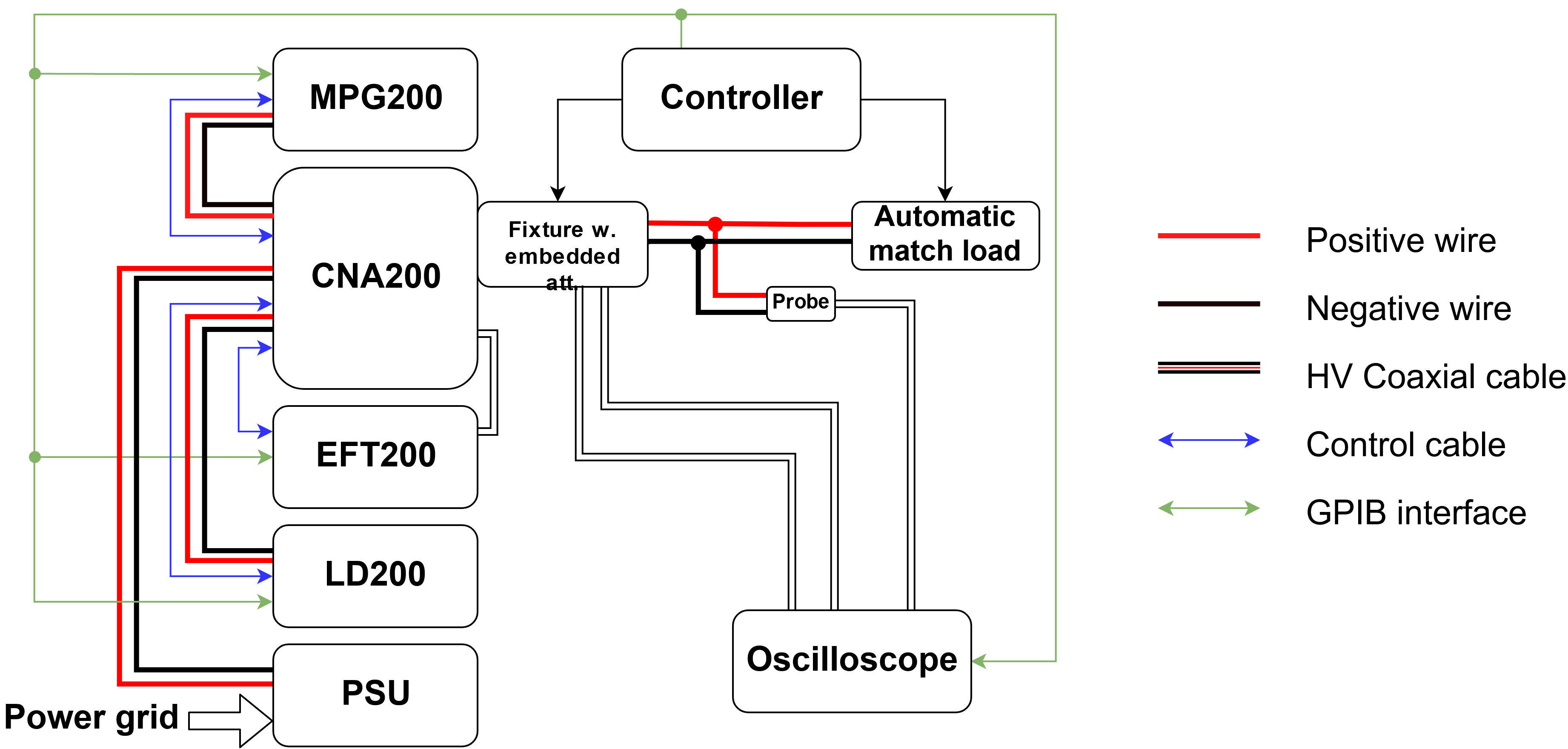
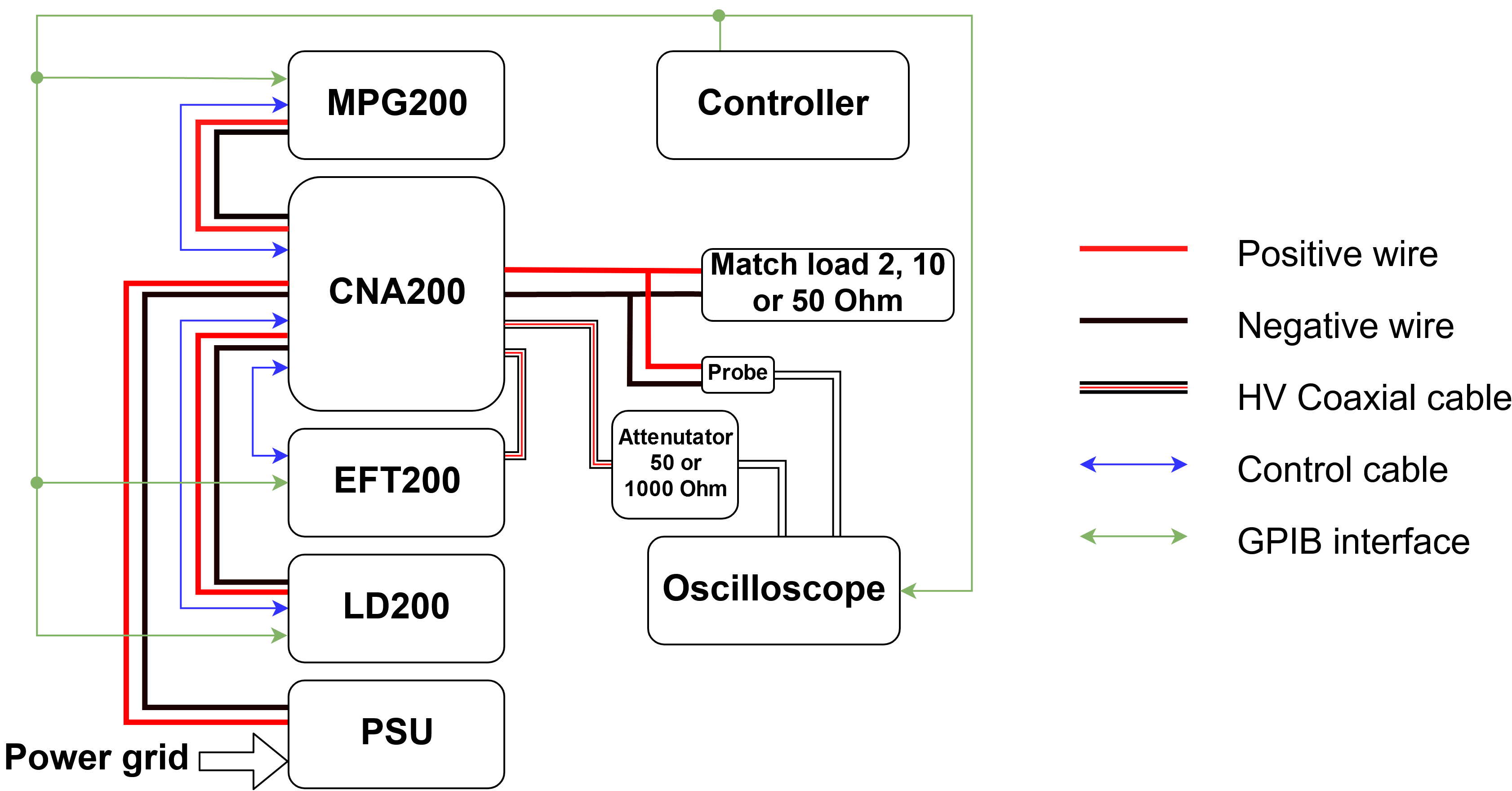
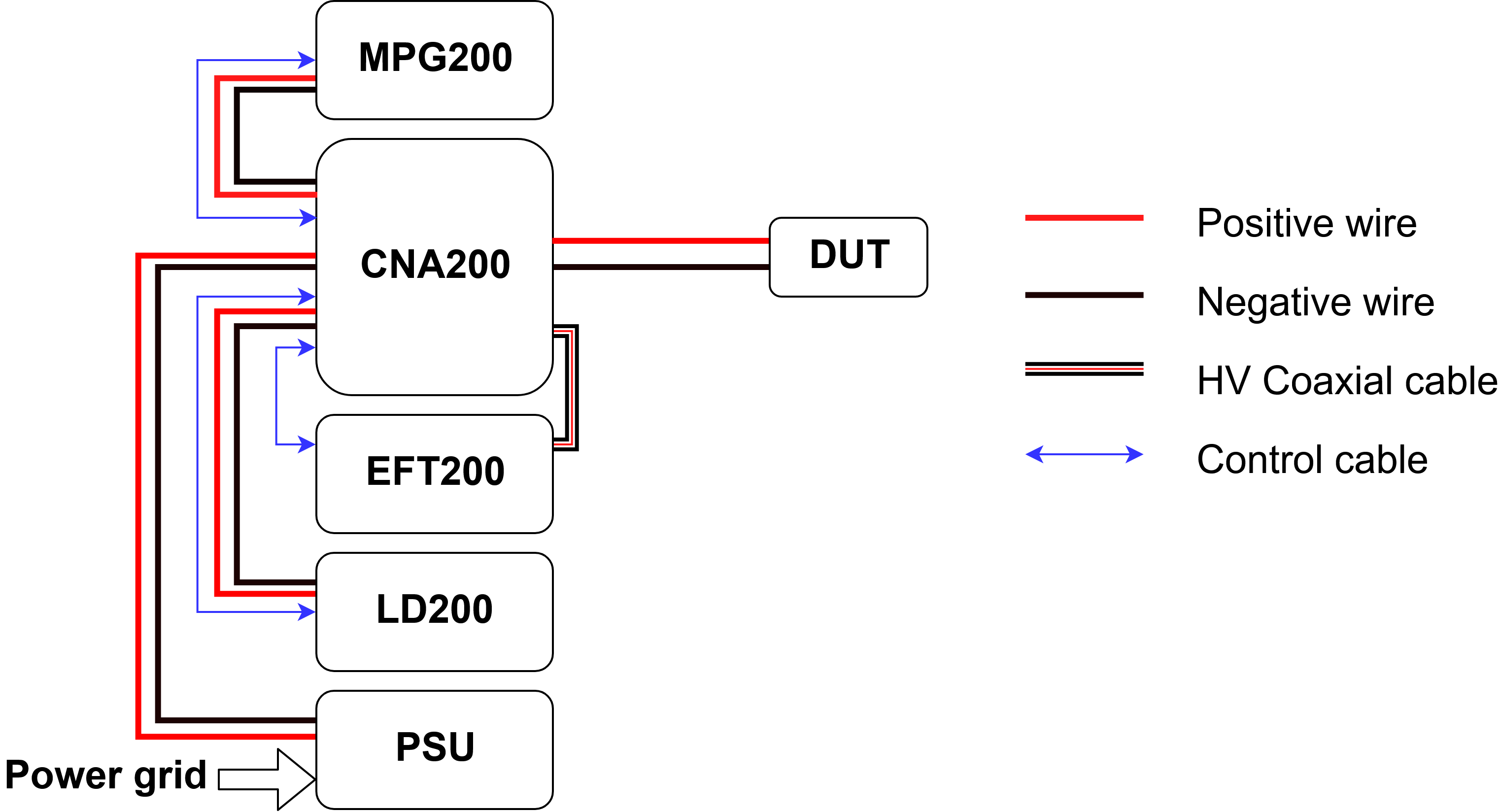
\caption{The CNA~200 allows each pusle generator to output their pulses through a common interface towards the DUT.}
|
|
\caption{The CNA~200 allows each pusle generator to output their pulses through a common interface towards the DUT.}
|
|
|
\label{fig:test_setup_cna_dut}
|
|
\label{fig:test_setup_cna_dut}
|
|
@@ -549,7 +550,7 @@ The SNA~200 is a coupling network used to multiplex the pulse generators outputs
|
|
|
\caption{Back.}
|
|
\caption{Back.}
|
|
|
\label{fig:cna200-back}
|
|
\label{fig:cna200-back}
|
|
|
\end{subfigure}
|
|
\end{subfigure}
|
|
|
- \caption{The CNA~200 is used to couple all of the other pulse generators outputs to a common output.}
|
|
|
|
|
|
|
+ \caption{The CNA~200 is used to couple all of the other pulse generators outputs to a common output. The generators are connected using wires with \SI{4}{\milli\meter} banana connectors, except for the EFT~200 which has a high-voltage coaxial connector. The blue arrows illustrates the control signals from the generators to the CNA~200.}
|
|
|
\label{fig:cna200}
|
|
\label{fig:cna200}
|
|
|
\end{figure}
|
|
\end{figure}
|
|
|
|
|
|